RIS-aided Wireless Communication with $1$-bit Discrete Optimization for Signal Enhancement
Paper and Code
Sep 12, 2022
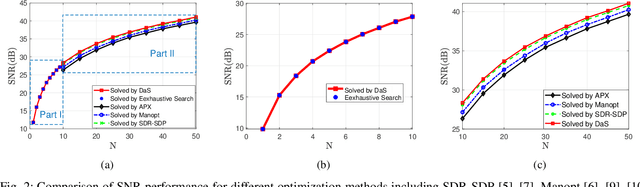
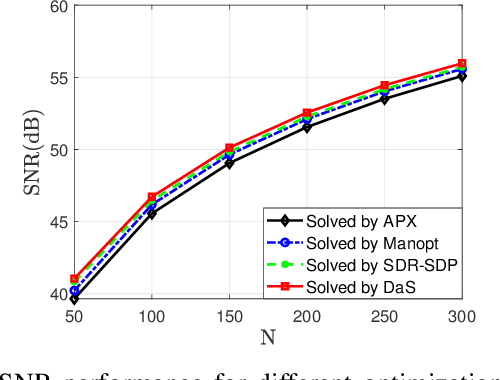

In recent years, a brand-new technology, reconfigurable intelligent surface (RIS) has been widely studied for reconfiguring the wireless propagation environment. RIS is an artificial surface of electromagnetic material that is capable of customizing the propagation of the wave impinging upon it. Utilizing RIS for communication service like signal enhancement usually lead to non-convex optimization problems. Existing optimization methods either suffers from scalability issues for $N$ number of RIS elements large, or may lead to suboptimal solutions in some scenario. In this paper, we propose a divide-and-sort (DaS) discrete optimization approach, that is guaranteed to find the global optimal phase shifts for $1$-bit RIS, and has time complexity $\mathcal{O}(N \log(N))$. Numerical experiments show that the proposed approach achieves a better ``performance--complexity tradeoff'' over other methods for $1$-bit RIS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge