Resource Allocation in a MAC with and without security via Game Theoretic Learning

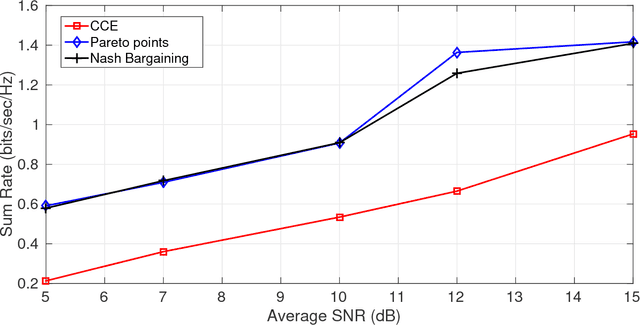
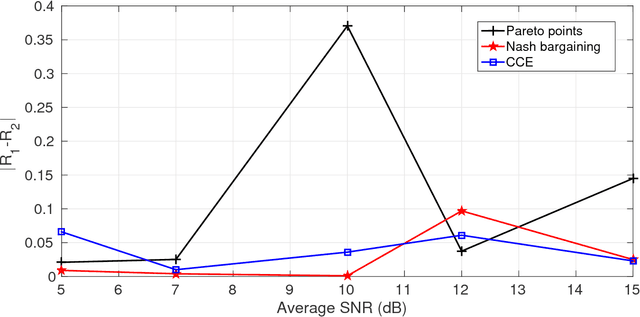
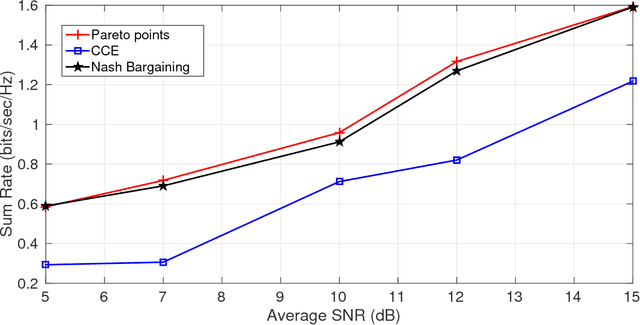
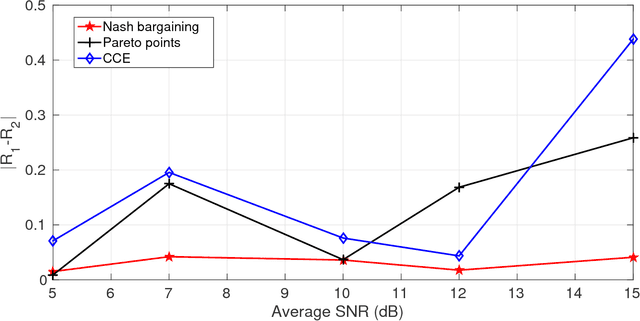
In this paper a $K$-user fading multiple access channel with and without security constraints is studied. First we consider a F-MAC without the security constraints. Under the assumption of individual CSI of users, we propose the problem of power allocation as a stochastic game when the receiver sends an ACK or a NACK depending on whether it was able to decode the message or not. We have used Multiplicative weight no-regret algorithm to obtain a Coarse Correlated Equilibrium (CCE). Then we consider the case when the users can decode ACK/NACK of each other. In this scenario we provide an algorithm to maximize the weighted sum-utility of all the users and obtain a Pareto optimal point. PP is socially optimal but may be unfair to individual users. Next we consider the case where the users can cooperate with each other so as to disagree with the policy which will be unfair to individual user. We then obtain a Nash bargaining solution, which in addition to being Pareto optimal, is also fair to each user. Next we study a $K$-user fading multiple access wiretap Channel with CSI of Eve available to the users. We use the previous algorithms to obtain a CCE, PP and a NBS. Next we consider the case where each user does not know the CSI of Eve but only its distribution. In that case we use secrecy outage as the criterion for the receiver to send an ACK or a NACK. Here also we use the previous algorithms to obtain a CCE, PP or a NBS. Finally we show that our algorithms can be extended to the case where a user can transmit at different rates. At the end we provide a few examples to compute different solutions and compare them under different CSI scenarios.