Removing Data Heterogeneity Influence Enhances Network Topology Dependence of Decentralized SGD

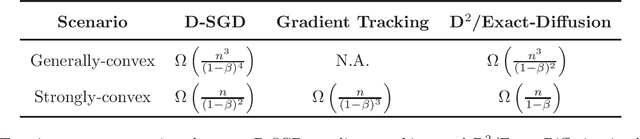
We consider decentralized stochastic optimization problems where a network of agents each owns a local cost function cooperate to find a minimizer of the global-averaged cost. A widely studied decentralized algorithm for this problem is D-SGD in which each node applies a stochastic gradient descent step, then averages its estimate with its neighbors. D-SGD is attractive due to its efficient single-iteration communication and can achieve linear speedup in convergence (in terms of the network size). However, D-SGD is very sensitive to the network topology. For smooth objective functions, the transient stage (which measures how fast the algorithm can reach the linear speedup stage) of D-SGD is on the order of $O(n/(1-\beta)^2)$ and $O(n^3/(1-\beta)^4)$ for strongly convex and generally convex cost functions, respectively, where $1-\beta \in (0,1)$ is a topology-dependent quantity that approaches $0$ for a large and sparse network. Hence, D-SGD suffers from slow convergence for large and sparse networks. In this work, we study the non-asymptotic convergence property of the D$^2$/Exact-diffusion algorithm. By eliminating the influence of data heterogeneity between nodes, D$^2$/Exact-diffusion is shown to have an enhanced transient stage that are on the order of $O(n/(1-\beta))$ and $O(n^3/(1-\beta)^2)$ for strongly convex and generally convex cost functions, respectively. Moreover, we provide a lower bound of the transient stage of D-SGD under homogeneous data distributions, which coincides with the transient stage of D$^2$/Exact-diffusion in the strongly-convex setting. These results show that removing the influence of data heterogeneity can ameliorate the network topology dependence of D-SGD. Compared with existing decentralized algorithms bounds, D$^2$/Exact-diffusion is least sensitive to network topology.