Recursive Rules with Aggregation: A Simple Unified Semantics

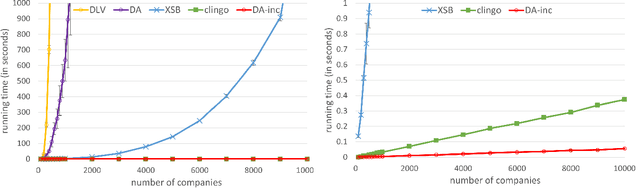
Complex reasoning problems are most clearly and easily specified using logical rules, especially recursive rules with aggregation such as counts and sums for practical applications. Unfortunately, the meaning of such rules has been a significant challenge, leading to many different conflicting semantics. This paper describes a unified semantics for recursive rules with aggregation, extending the unified founded semantics and constraint semantics for recursive rules with negation. The key idea is to support simple expression of the different assumptions underlying different semantics, and orthogonally interpret aggregation operations straightforwardly using their simple usual meaning.