Reconstruction of observed mechanical motions with Artificial Intelligence tools
Paper and Code
Feb 23, 2022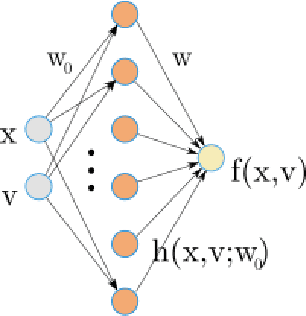
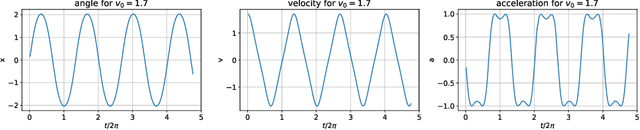
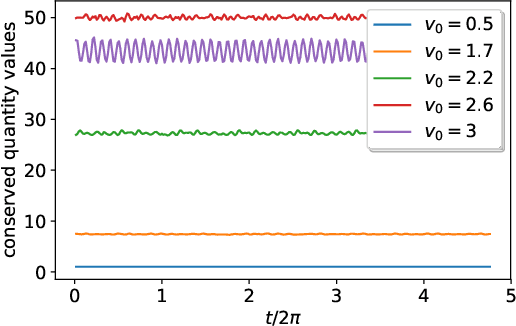
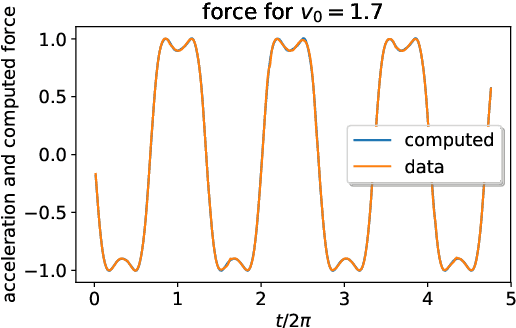
The goal of this paper is to determine the laws of observed trajectories assuming that there is a mechanical system in the background and using these laws to continue the observed motion in a plausible way. The laws are represented by neural networks with a limited number of parameters. The training of the networks follows the Extreme Learning Machine idea. We determine laws for different levels of embedding, thus we can represent not only the equation of motion but also the symmetries of different kinds. In the recursive numerical evolution of the system, we require the fulfillment of all the observed laws, within the determined numerical precision. In this way, we can successfully reconstruct both integrable and chaotic motions, as we demonstrate in the example of the gravity pendulum and the double pendulum.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge