Rapid Vector-based Any-angle Path Planning with Non-convex Obstacles
Paper and Code
Aug 11, 2024
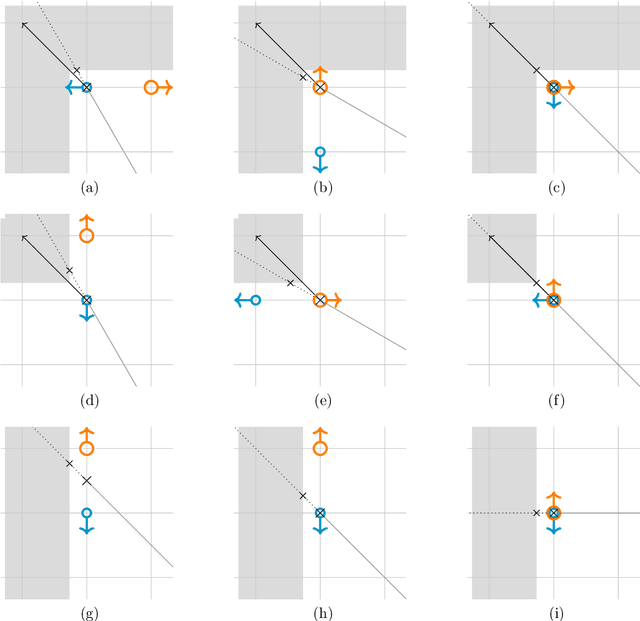
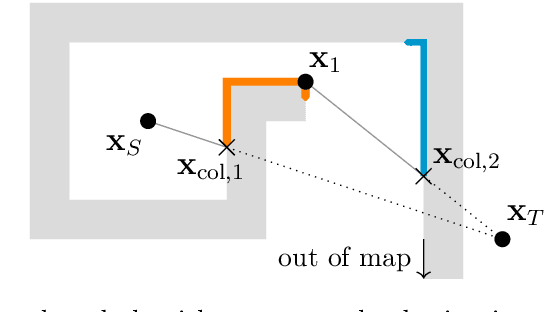
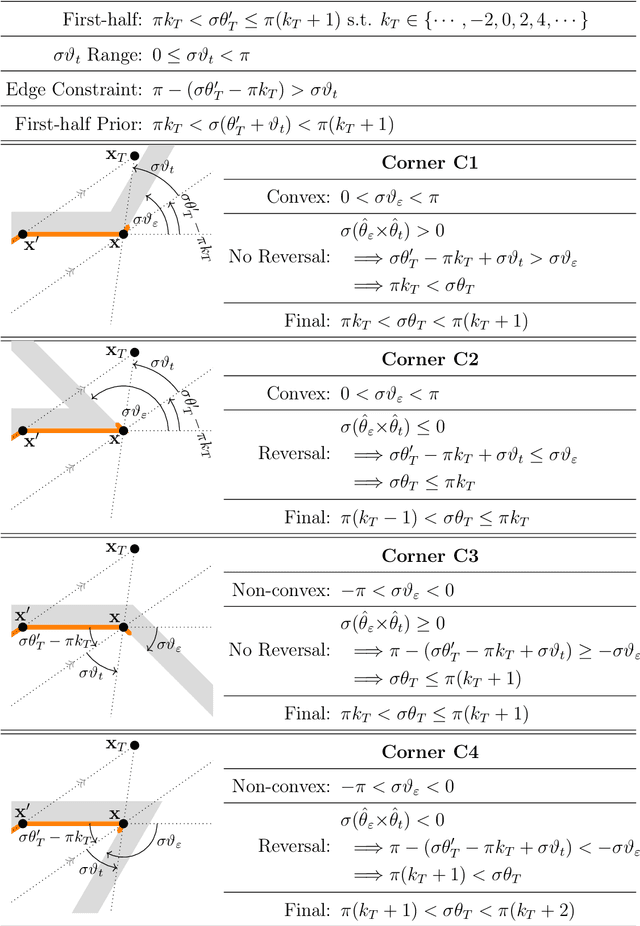
Vector-based algorithms are novel algorithms in optimal any-angle path planning that are motivated by bug algorithms, bypassing free space by directly conducting line-of-sight checks between two queried points, and searching along obstacle contours if a check collides with an obstacle. The algorithms outperform conventional free-space planners such as A* especially when the queried points are far apart. The thesis presents novel search methods to speed up vector-based algorithms in non-convex obstacles by delaying line-of-sight checks. The "best hull" is a notable method that allows for monotonically increasing path cost estimates even without verifying line-of-sight, utilizing "phantom points" placed on non-convex corners to mimic future turning points. Building upon the methods, the algorithms R2 and R2+ are formulated, which outperform other vector-based algorithms when the optimal path solution is expected to have few turning points. Other novel methods include a novel and versatile multi-dimensional ray tracer for occupancy grids, and a description of the three-dimensional angular sector for future works.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge