Random Shuffling Beats SGD Only After Many Epochs on Ill-Conditioned Problems
Paper and Code
Jun 12, 2021
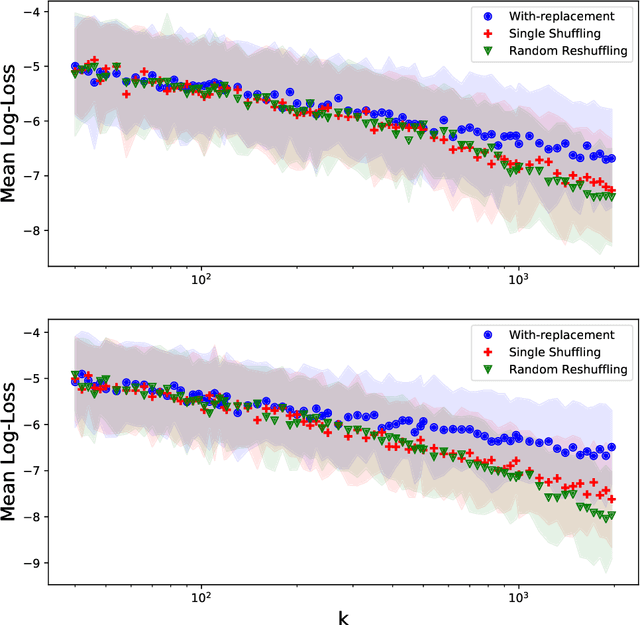
Recently, there has been much interest in studying the convergence rates of without-replacement SGD, and proving that it is faster than with-replacement SGD in the worst case. However, these works ignore or do not provide tight bounds in terms of the problem's geometry, including its condition number. Perhaps surprisingly, we prove that when the condition number is taken into account, without-replacement SGD \emph{does not} significantly improve on with-replacement SGD in terms of worst-case bounds, unless the number of epochs (passes over the data) is larger than the condition number. Since many problems in machine learning and other areas are both ill-conditioned and involve large datasets, this indicates that without-replacement does not necessarily improve over with-replacement sampling for realistic iteration budgets. We show this by providing new lower and upper bounds which are tight (up to log factors), for quadratic problems with commuting quadratic terms, precisely quantifying the dependence on the problem parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge