Random Matrix-Improved Estimation of the Wasserstein Distance between two Centered Gaussian Distributions
Paper and Code
Mar 08, 2019
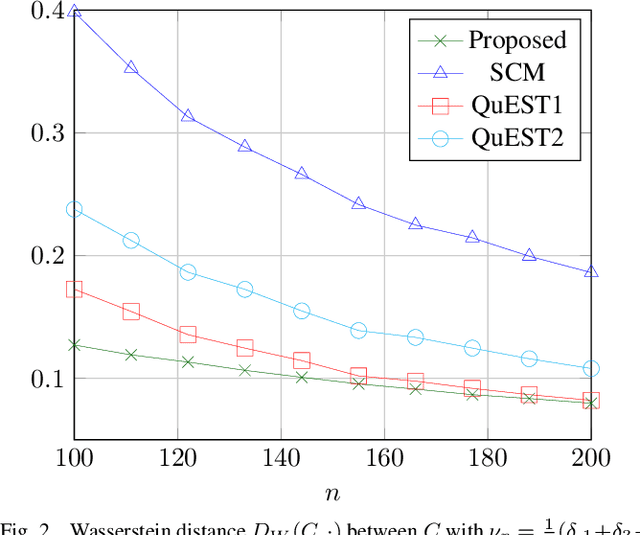
This article proposes a method to consistently estimate functionals $\frac1p\sum_{i=1}^pf(\lambda_i(C_1C_2))$ of the eigenvalues of the product of two covariance matrices $C_1,C_2\in\mathbb{R}^{p\times p}$ based on the empirical estimates $\lambda_i(\hat C_1\hat C_2)$ ($\hat C_a=\frac1{n_a}\sum_{i=1}^{n_a} x_i^{(a)}x_i^{(a){{\sf T}}}$), when the size $p$ and number $n_a$ of the (zero mean) samples $x_i^{(a)}$ are similar. As a corollary, a consistent estimate of the Wasserstein distance (related to the case $f(t)=\sqrt{t}$) between centered Gaussian distributions is derived. The new estimate is shown to largely outperform the classical sample covariance-based `plug-in' estimator. Based on this finding, a practical application to covariance estimation is then devised which demonstrates potentially significant performance gains with respect to state-of-the-art alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge