Quantum-inspired canonical correlation analysis for exponentially large dimensional data
Paper and Code
Jul 07, 2019
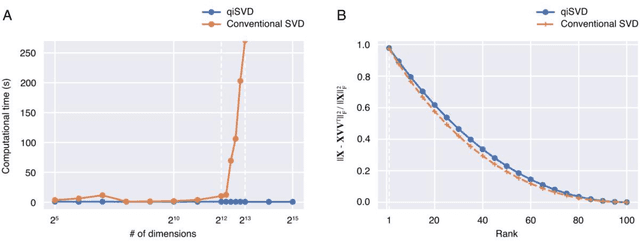
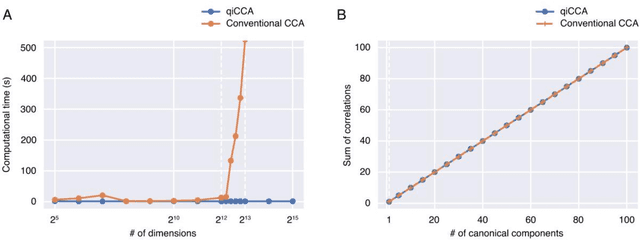

Canonical correlation analysis (CCA) is a technique to find statistical dependencies between a pair of multivariate data. However, its application to high dimensional data is limited due to the resulting time complexity. While the conventional CCA algorithm requires polynomial time, we have developed an algorithm that approximates CCA with computational time proportional to the logarithm of the input dimensionality using quantum-inspired computation. The computational efficiency and approximation performance of the proposed quantum-inspired CCA (qiCCA) algorithm are experimentally demonstrated. Furthermore, the fast computation of qiCCA allows us to directly apply CCA even after nonlinearly mapping raw input data into very high dimensional spaces. Experiments performed using a benchmark dataset demonstrated that, by mapping the raw input data into the high dimensional spaces with second-order monomials, the proposed qiCCA extracted more correlations than linear CCA and was comparable to deep CCA and kernel CCA. These results suggest that qiCCA is considerably useful and quantum-inspired computation has the potential to unlock a new field in which exponentially large dimensional data can be analyzed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge