Provably Accurate Double-Sparse Coding
Paper and Code
Dec 12, 2017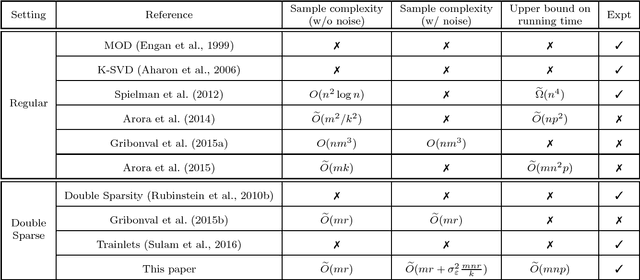
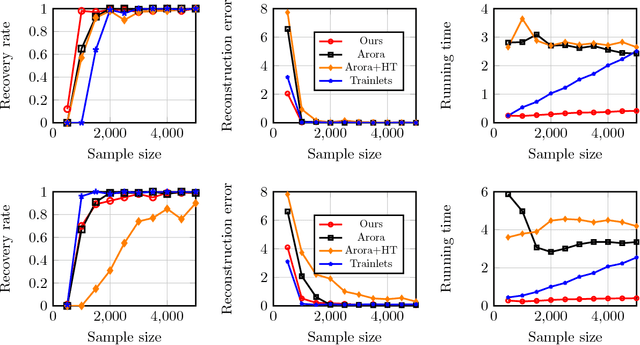
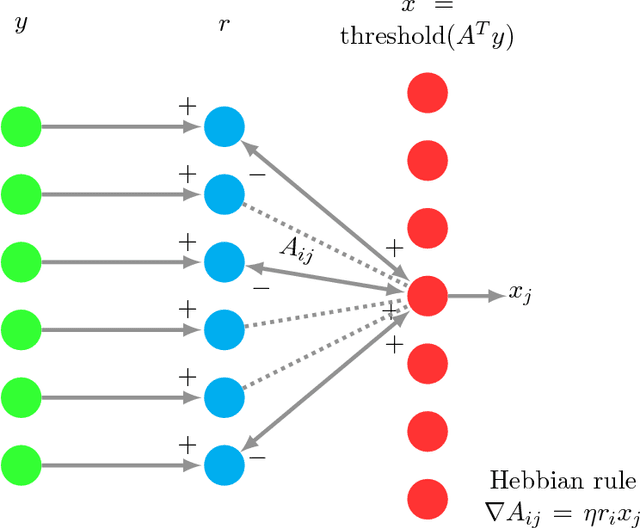
Sparse coding is a crucial subroutine in algorithms for various signal processing, deep learning, and other machine learning applications. The central goal is to learn an overcomplete dictionary that can sparsely represent a given input dataset. However, a key challenge is that storage, transmission, and processing of the learned dictionary can be untenably high if the data dimension is high. In this paper, we consider the double-sparsity model introduced by Rubinstein et al. (2010b) where the dictionary itself is the product of a fixed, known basis and a data-adaptive sparse component. First, we introduce a simple algorithm for double-sparse coding that can be amenable to efficient implementation via neural architectures. Second, we theoretically analyze its performance and demonstrate asymptotic sample complexity and running time benefits over existing (provable) approaches for sparse coding. To our knowledge, our work introduces the first computationally efficient algorithm for double-sparse coding that enjoys rigorous statistical guarantees. Finally, we support our analysis via several numerical experiments on simulated data, confirming that our method can indeed be useful in problem sizes encountered in practical applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge