Projected Gradient Descent Algorithms for Solving Nonlinear Inverse Problems with Generative Priors
Paper and Code
Sep 21, 2022

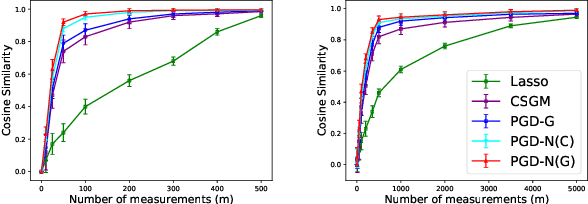

In this paper, we propose projected gradient descent (PGD) algorithms for signal estimation from noisy nonlinear measurements. We assume that the unknown $p$-dimensional signal lies near the range of an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs. In particular, we consider two cases when the nonlinear link function is either unknown or known. For unknown nonlinearity, similarly to \cite{liu2020generalized}, we make the assumption of sub-Gaussian observations and propose a linear least-squares estimator. We show that when there is no representation error and the sensing vectors are Gaussian, roughly $O(k \log L)$ samples suffice to ensure that a PGD algorithm converges linearly to a point achieving the optimal statistical rate using arbitrary initialization. For known nonlinearity, we assume monotonicity as in \cite{yang2016sparse}, and make much weaker assumptions on the sensing vectors and allow for representation error. We propose a nonlinear least-squares estimator that is guaranteed to enjoy an optimal statistical rate. A corresponding PGD algorithm is provided and is shown to also converge linearly to the estimator using arbitrary initialization. In addition, we present experimental results on image datasets to demonstrate the performance of our PGD algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge