Positional Encoder Graph Neural Networks for Geographic Data
Paper and Code
Nov 19, 2021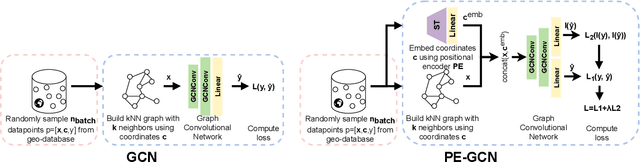
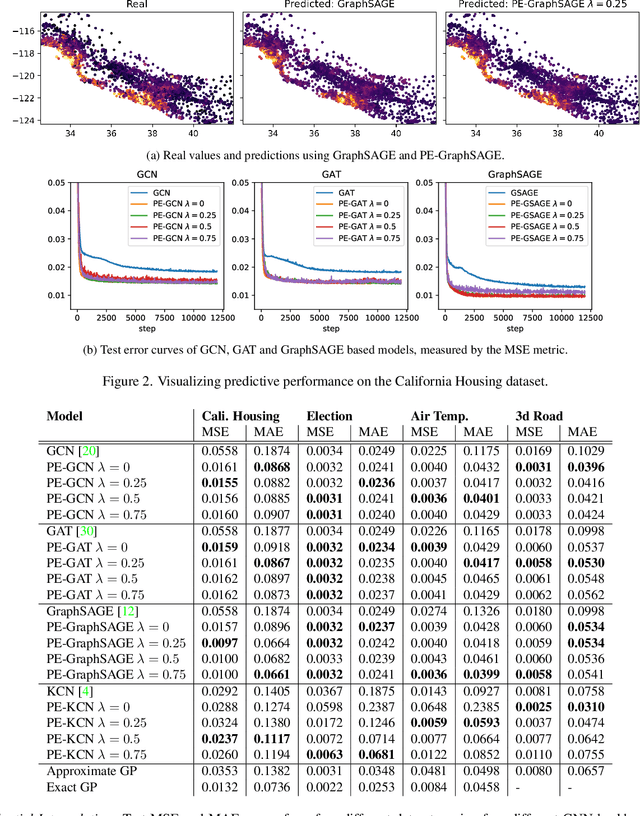


Graph neural networks (GNNs) provide a powerful and scalable solution for modeling continuous spatial data. However, in the absence of further context on the geometric structure of the data, they often rely on Euclidean distances to construct the input graphs. This assumption can be improbable in many real-world settings, where the spatial structure is more complex and explicitly non-Euclidean (e.g., road networks). In this paper, we propose PE-GNN, a new framework that incorporates spatial context and correlation explicitly into the models. Building on recent advances in geospatial auxiliary task learning and semantic spatial embeddings, our proposed method (1) learns a context-aware vector encoding of the geographic coordinates and (2) predicts spatial autocorrelation in the data in parallel with the main task. On spatial regression tasks, we show the effectiveness of our approach, improving performance over different state-of-the-art GNN approaches. We also test our approach for spatial interpolation, i.e., spatial regression without node features, a task that GNNs are currently not competitive at. We observe that our approach not only vastly improves over the GNN baselines, but can match Gaussian processes, the most commonly utilized method for spatial interpolation problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge