PoPE: Legendre Orthogonal Polynomials Based Position Encoding for Large Language Models
Paper and Code
Apr 29, 2024
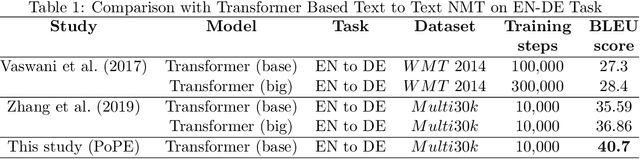


There are several improvements proposed over the baseline Absolute Positional Encoding (APE) method used in original transformer. In this study, we aim to investigate the implications of inadequately representing positional encoding in higher dimensions on crucial aspects of the attention mechanism, the model's capacity to learn relative positional information, and the convergence of models, all stemming from the choice of sinusoidal basis functions. Through a combination of theoretical insights and empirical analyses, we elucidate how these challenges extend beyond APEs and may adversely affect the performance of Relative Positional Encoding (RPE) methods, such as Rotatory Positional Encoding (RoPE). Subsequently, we introduce an innovative solution termed Orthogonal Polynomial Based Positional Encoding (PoPE) to address some of the limitations associated with existing methods. The PoPE method encodes positional information by leveraging Orthogonal Legendre polynomials. Legendre polynomials as basis functions offers several desirable properties for positional encoding, including improved correlation structure, non-periodicity, orthogonality, and distinct functional forms among polynomials of varying orders. Our experimental findings demonstrate that transformer models incorporating PoPE outperform baseline transformer models on the $Multi30k$ English-to-German translation task, thus establishing a new performance benchmark. Furthermore, PoPE-based transformers exhibit significantly accelerated convergence rates. Additionally, we will present novel theoretical perspectives on position encoding based on the superior performance of PoPE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge