Planning With Discrete Harmonic Potential Fields
Paper and Code
Aug 21, 2016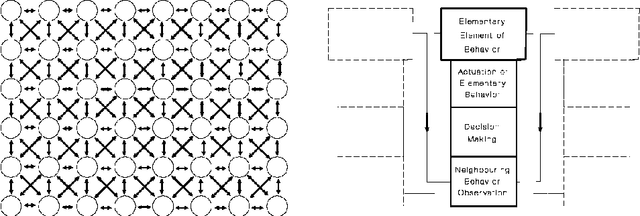
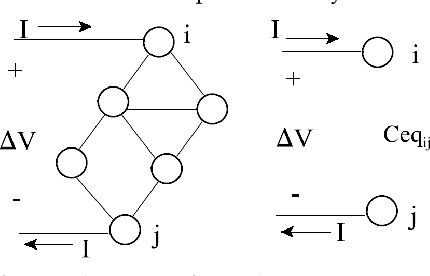
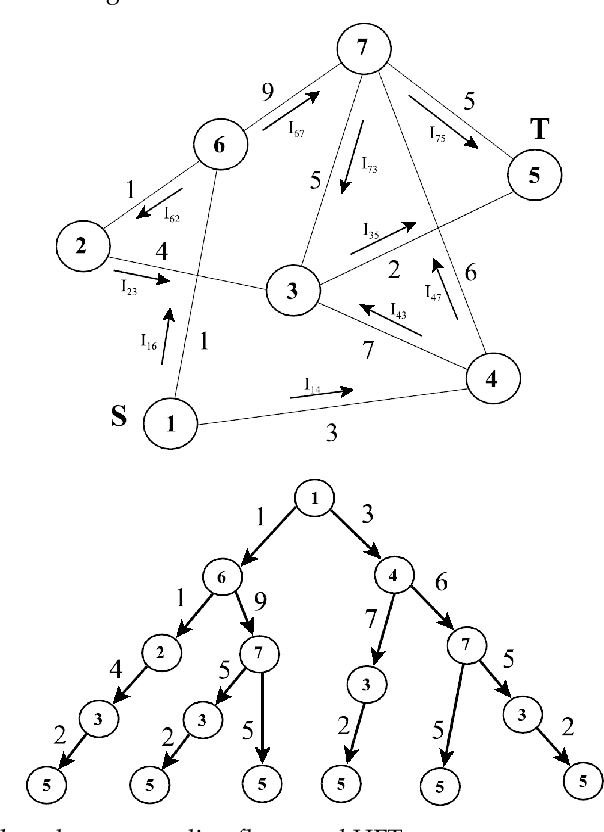
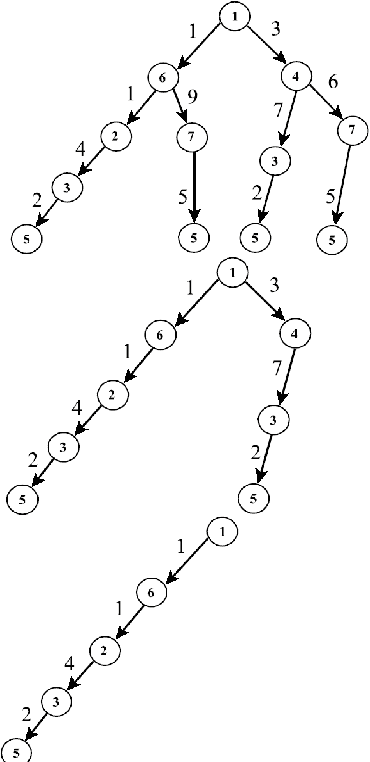
In this work a discrete counterpart to the continuous harmonic potential field approach is suggested. The extension to the discrete case makes use of the strong relation HPF-based planning has to connectionist artificial intelligence (AI). Connectionist AI systems are networks of simple, interconnected processors running in parallel within the confines of the environment in which the planning action is to be synthesized. It is not hard to see that such a paradigm naturally lends itself to planning on weighted graphs where the processors may be seen as the vertices of the graph and the relations among them as its edges. Electrical networks are an effective realization of connectionist AI. The utility of the discrete HPF (DHPF) approach is demonstrated in three ways. First, the capability of the DHPF approach to generate new, abstract, planning techniques is demonstrated by constructing a novel, efficient, optimal, discrete planning method called the M* algorithm. Also, its ability to augment the capabilities of existing planners is demonstrated by suggesting a generic solution to the lower bound problem faced by the A* algorithm. The DHPF approach is shown to be useful in solving specific planning problems in communication. It is demonstrated that the discrete HPF paradigm can support routing on-the-fly while the network is still in a transient state. It is shown by simulation that if a path to the target always exist and the switching delays in the routers are negligible, a packet will reach its destination despite the changes in the network which may simultaneously take place while the packet is being routed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge