Physics-constrained 3D Convolutional Neural Networks for Electrodynamics

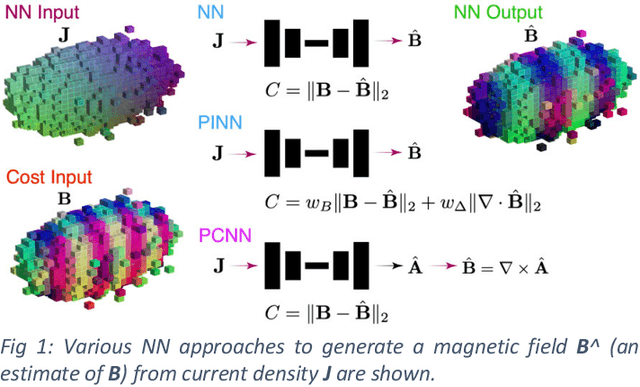
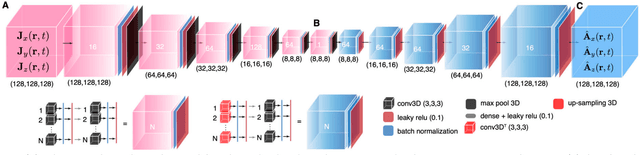
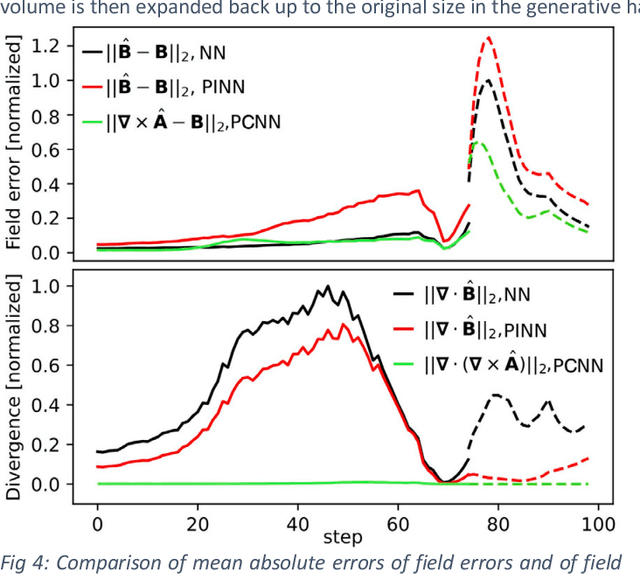
We present a physics-constrained neural network (PCNN) approach to solving Maxwell's equations for the electromagnetic fields of intense relativistic charged particle beams. We create a 3D convolutional PCNN to map time-varying current and charge densities J(r,t) and p(r,t) to vector and scalar potentials A(r,t) and V(r,t) from which we generate electromagnetic fields according to Maxwell's equations: B=curl(A), E=-div(V)-dA/dt. Our PCNNs satisfy hard constraints, such as div(B)=0, by construction. Soft constraints push A and V towards satisfying the Lorenz gauge.