Phase Transitions and Backbones of the Asymmetric Traveling Salesman Problem

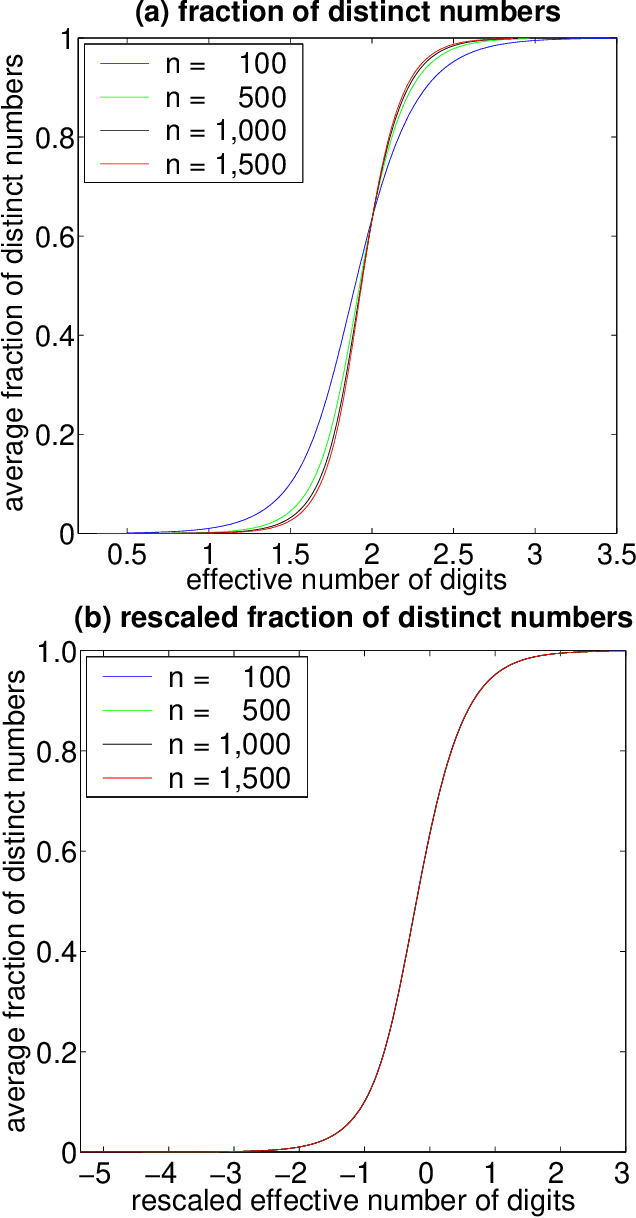
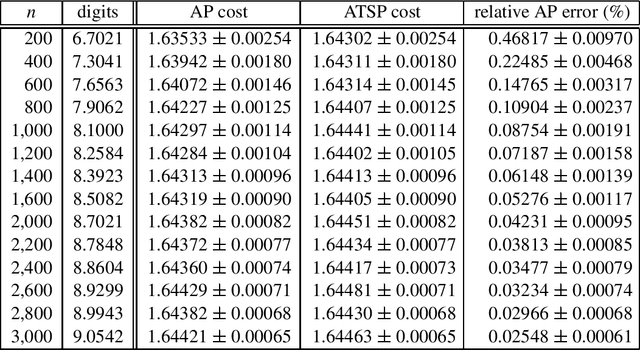
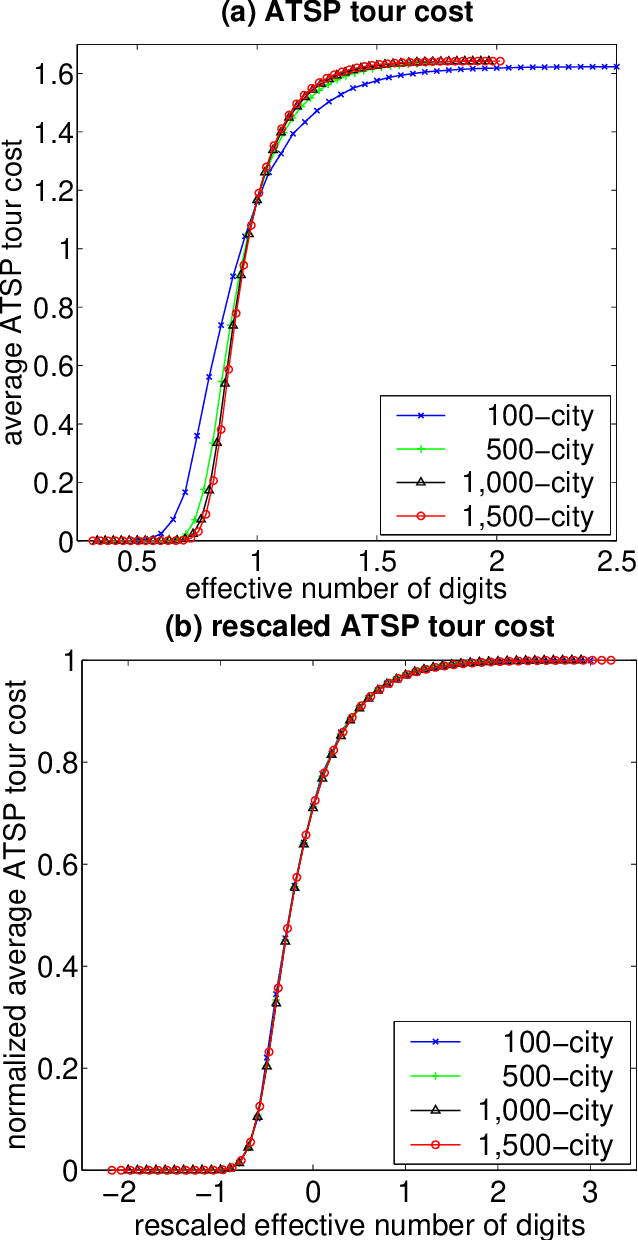
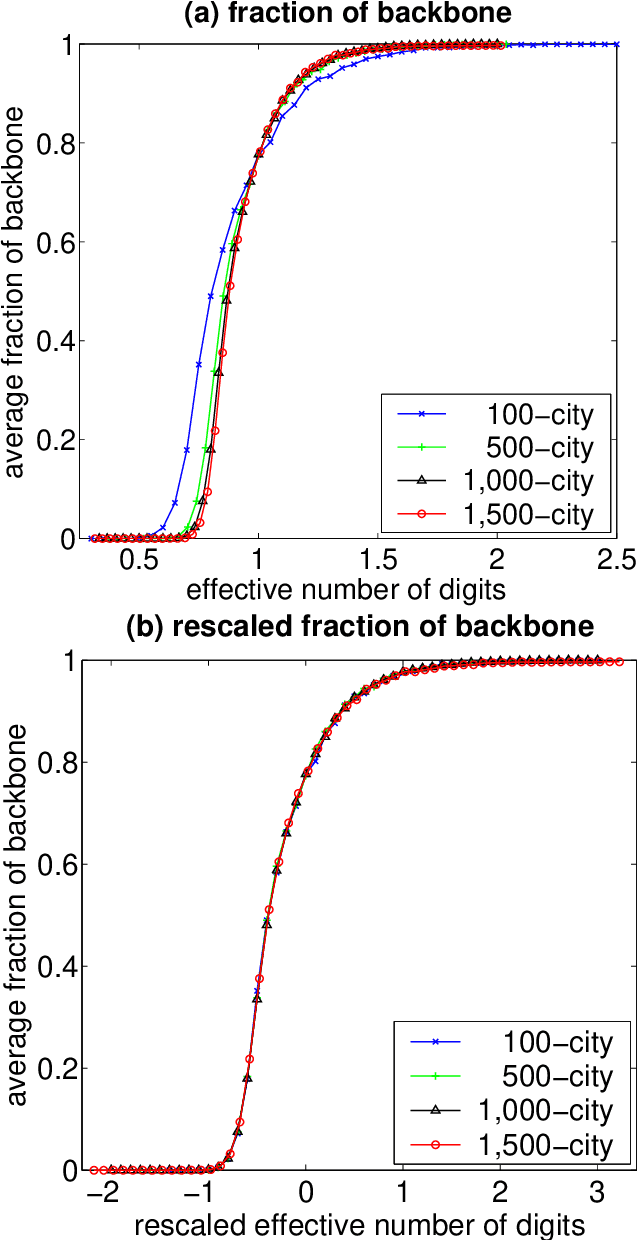
In recent years, there has been much interest in phase transitions of combinatorial problems. Phase transitions have been successfully used to analyze combinatorial optimization problems, characterize their typical-case features and locate the hardest problem instances. In this paper, we study phase transitions of the asymmetric Traveling Salesman Problem (ATSP), an NP-hard combinatorial optimization problem that has many real-world applications. Using random instances of up to 1,500 cities in which intercity distances are uniformly distributed, we empirically show that many properties of the problem, including the optimal tour cost and backbone size, experience sharp transitions as the precision of intercity distances increases across a critical value. Our experimental results on the costs of the ATSP tours and assignment problem agree with the theoretical result that the asymptotic cost of assignment problem is pi ^2 /6 the number of cities goes to infinity. In addition, we show that the average computational cost of the well-known branch-and-bound subtour elimination algorithm for the problem also exhibits a thrashing behavior, transitioning from easy to difficult as the distance precision increases. These results answer positively an open question regarding the existence of phase transitions in the ATSP, and provide guidance on how difficult ATSP problem instances should be generated.