Phase Retrieval via Incremental Truncated Wirtinger Flow
Paper and Code
Jun 10, 2016
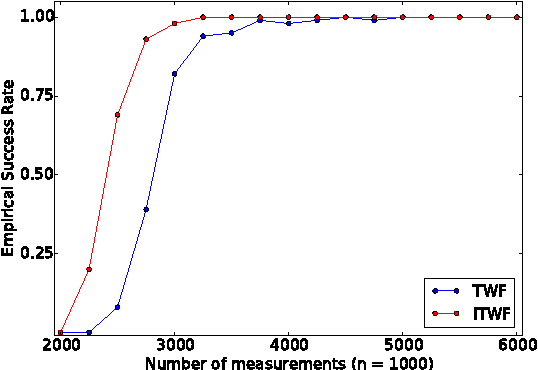
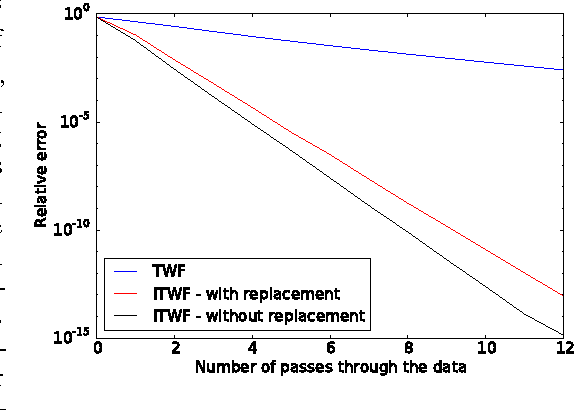
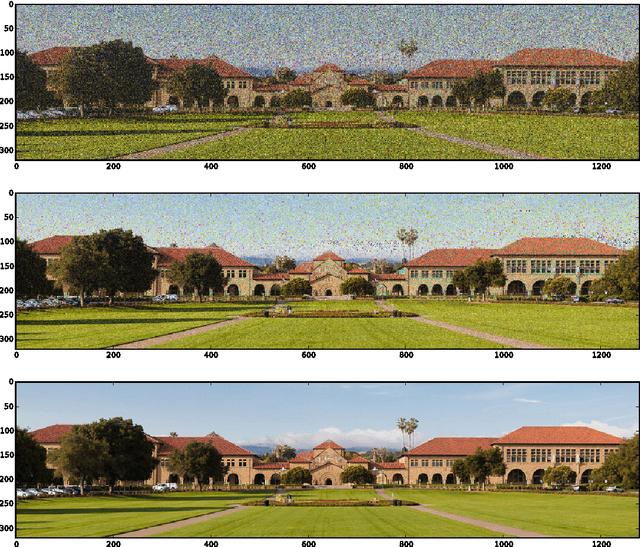
In the phase retrieval problem, an unknown vector is to be recovered given quadratic measurements. This problem has received considerable attention in recent times. In this paper, we present an algorithm to solve a nonconvex formulation of the phase retrieval problem, that we call $\textit{Incremental Truncated Wirtinger Flow}$. Given random Gaussian sensing vectors, we prove that it converges linearly to the solution, with an optimal sample complexity. We also provide stability guarantees of the algorithm under noisy measurements. Performance and comparisons with existing algorithms are illustrated via numerical experiments on simulated and real data, with both random and structured sensing vectors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge