Pendant Drop Tensiometry: A Machine Learning Approach
Paper and Code
Jun 17, 2020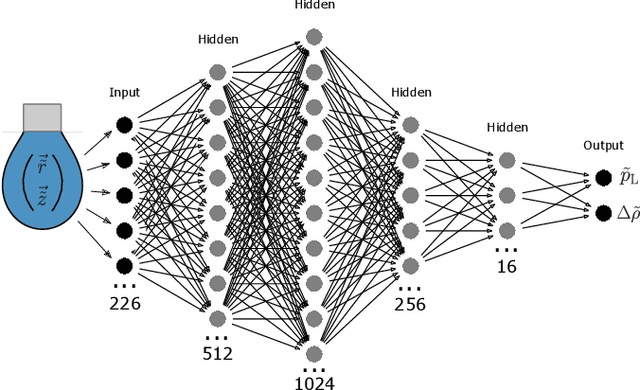
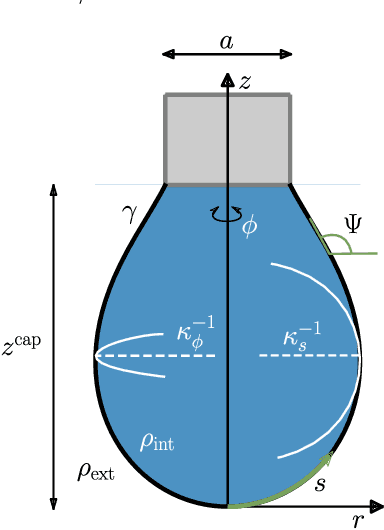
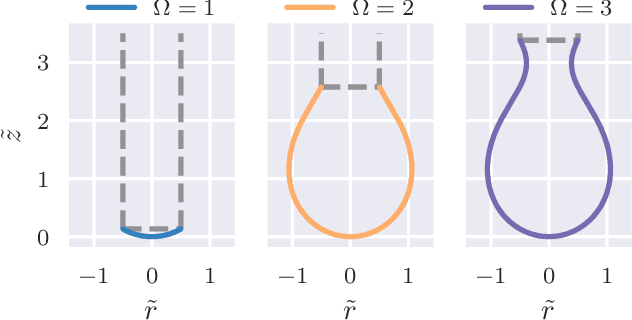
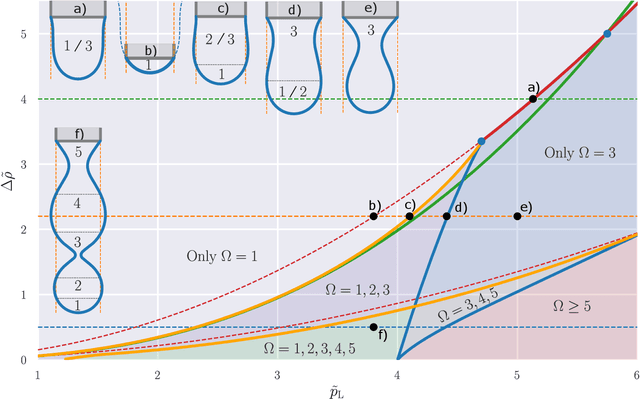
Modern pendant drop tensiometry relies on numerical solution of the Young-Laplace equation and allow to determine the surface tension from a single picture of a pendant drop with high precision. Most of these techniques solve the Young-Laplace equation many times over to find the material parameters that provide a fit to a supplied image of a real droplet. Here we introduce a machine learning approach to solve this problem in a computationally more efficient way. We train a deep neural network to determine the surface tension of a given droplet shape using a large training set of numerically generated droplet shapes. We show that the deep learning approach is superior to the current state of the art shape fitting approach in speed and precision, in particular if shapes in the training set reflect the sensitivity of the droplet shape with respect to surface tension. In order to derive such an optimized training set we clarify the role of the Worthington number as quality indicator in conventional shape fitting and in the machine learning approach. Our approach demonstrates the capabilities of deep neural networks in the material parameter determination from rheological deformation experiments in general.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge