Out-of-sample error estimate for robust M-estimators with convex penalty
Paper and Code
Sep 14, 2020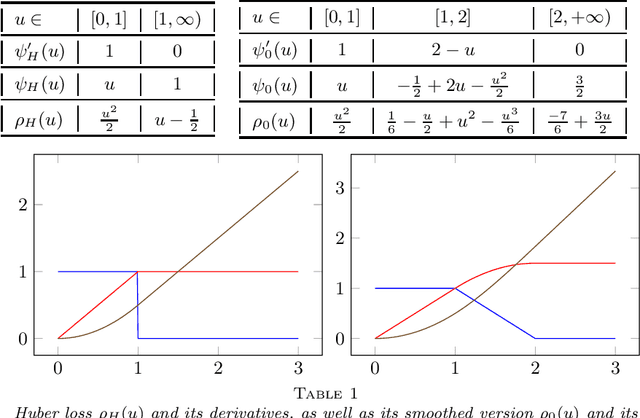
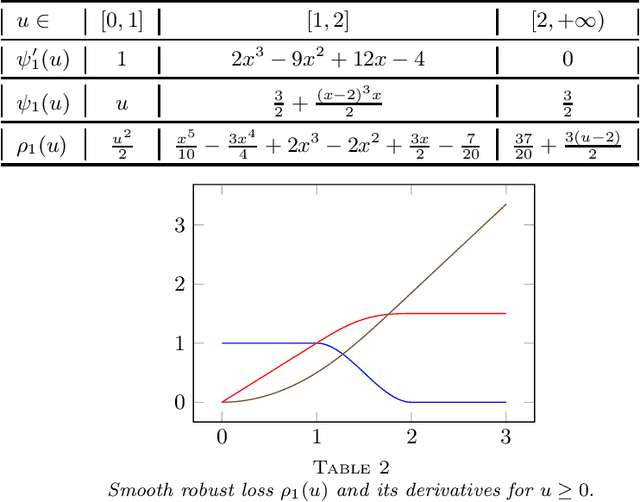
A generic out-of-sample error estimate is proposed for robust $M$-estimators regularized with a convex penalty in high-dimensional linear regression where $(X,y)$ is observed and $p,n$ are of the same order. If $\psi$ is the derivative of the robust data-fitting loss $\rho$, the estimate depends on the observed data only through the quantities $\hat\psi = \psi(y-X\hat\beta)$, $X^\top \hat\psi$ and the derivatives $(\partial/\partial y) \hat\psi$ and $(\partial/\partial y) X\hat\beta$ for fixed $X$. The out-of-sample error estimate enjoys a relative error of order $n^{-1/2}$ in a linear model with Gaussian covariates and independent noise, either non-asymptotically when $p/n\le \gamma$ or asymptotically in the high-dimensional asymptotic regime $p/n\to\gamma'\in(0,\infty)$. General differentiable loss functions $\rho$ are allowed provided that $\psi=\rho'$ is 1-Lipschitz. The validity of the out-of-sample error estimate holds either under a strong convexity assumption, or for the $\ell_1$-penalized Huber M-estimator if the number of corrupted observations and sparsity of the true $\beta$ are bounded from above by $s_*n$ for some small enough constant $s_*\in(0,1)$ independent of $n,p$. For the square loss and in the absence of corruption in the response, the results additionally yield $n^{-1/2}$-consistent estimates of the noise variance and of the generalization error. This generalizes, to arbitrary convex penalty, estimates that were previously known for the Lasso.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge