Optimum classical beam position sensing
Paper and Code
Feb 01, 2024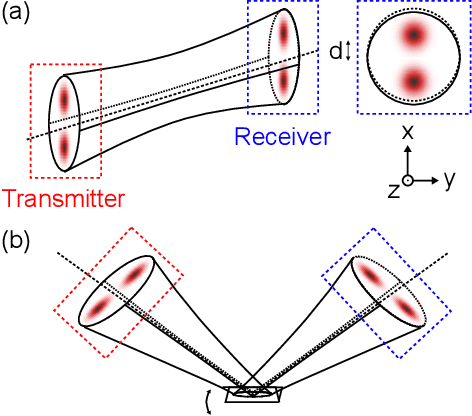
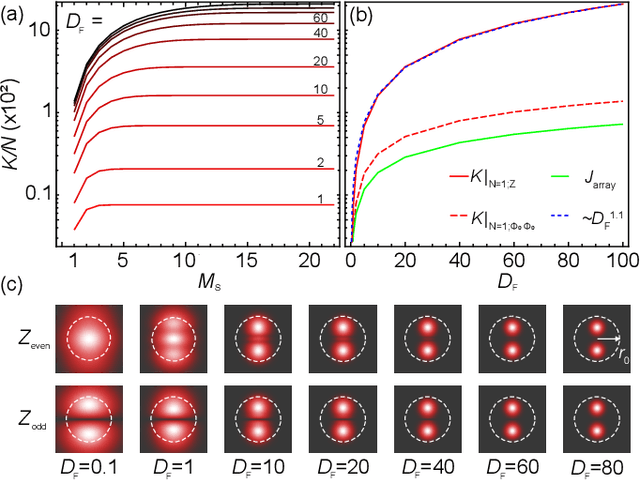
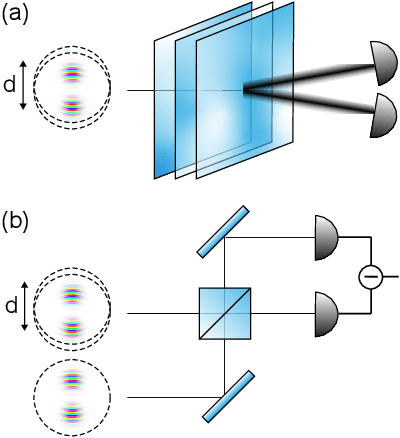
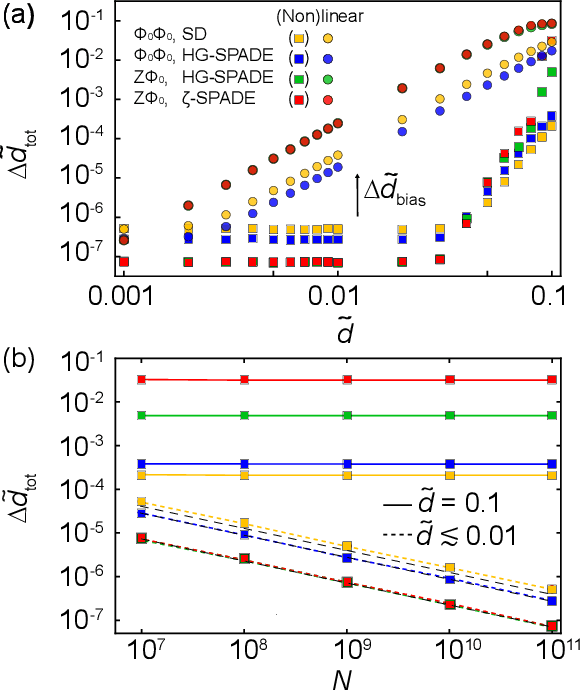
Beam displacement measurements are widely used in optical sensing and communications; however, their performance is affected by numerous intrinsic and extrinsic factors including beam profile, propagation loss, and receiver architecture. Here we present a framework for designing a classically optimal beam displacement transceiver, using quantum estimation theory. We consider the canonical task of estimating the position of a diffraction-limited laser beam after passing through an apertured volume characterized by Fresnel-number product DF. As a rule of thumb, higher-order Gaussian modes provide more information about beam displacement, but are more sensitive to loss. Applying quantum Fisher information, we design mode combinations that optimally leverage this trade-off, and show that a greater than 10-fold improvement in precision is possible, relative to the fundamental mode, for a practically relevant DF = 100. We also show that this improvement is realizable with a variety of practical receiver architectures. Our findings extend previous works on lossless transceivers, may have immediate impact on applications such as atomic force microscopy and near-field optical communication, and pave the way towards globally optimal transceivers using non-classical laser fields.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge