Optimal input representation in neural systems at the edge of chaos
Paper and Code
Jul 12, 2021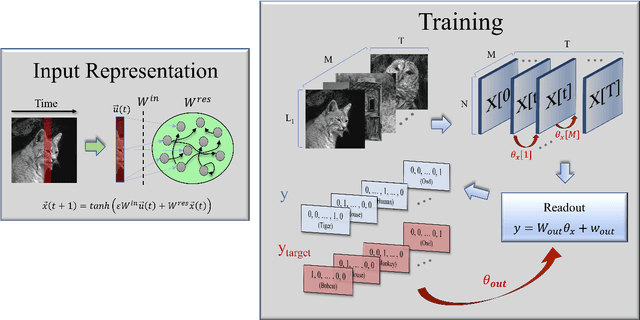
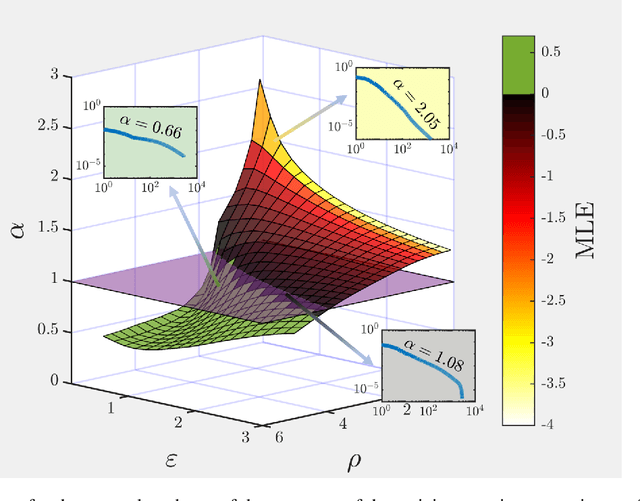
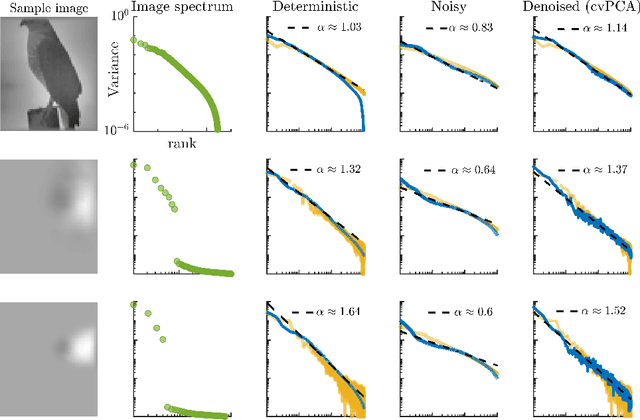
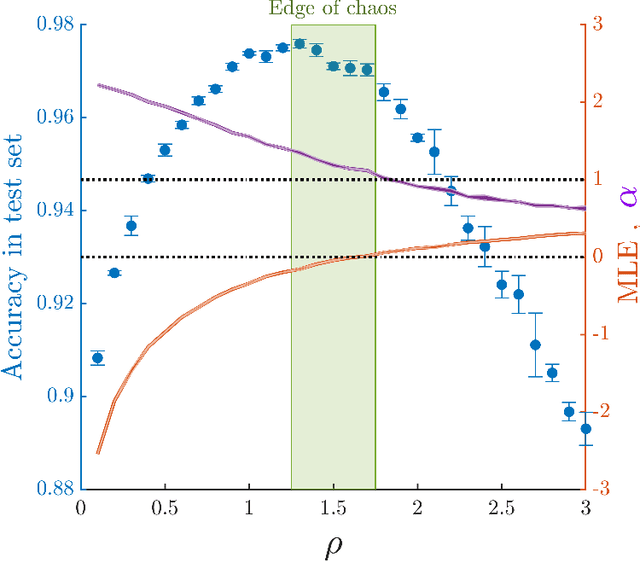
Shedding light onto how biological systems represent, process and store information in noisy environments is a key and challenging goal. A stimulating, though controversial, hypothesis poses that operating in dynamical regimes near the edge of a phase transition, i.e. at criticality or the "edge of chaos", can provide information-processing living systems with important operational advantages, creating, e.g., an optimal trade-off between robustness and flexibility. Here, we elaborate on a recent theoretical result, which establishes that the spectrum of covariance matrices of neural networks representing complex inputs in a robust way needs to decay as a power-law of the rank, with an exponent close to unity, a result that has been indeed experimentally verified in neurons of the mouse visual cortex. Aimed at understanding and mimicking these results, we construct an artificial neural network and train it to classify images. Remarkably, we find that the best performance in such a task is obtained when the network operates near the critical point, at which the eigenspectrum of the covariance matrix follows the very same statistics as actual neurons do. Thus, we conclude that operating near criticality can also have -- besides the usually alleged virtues -- the advantage of allowing for flexible, robust and efficient input representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge