Optimal DNN Primitive Selection with Partitioned Boolean Quadratic Programming
Paper and Code
Nov 02, 2018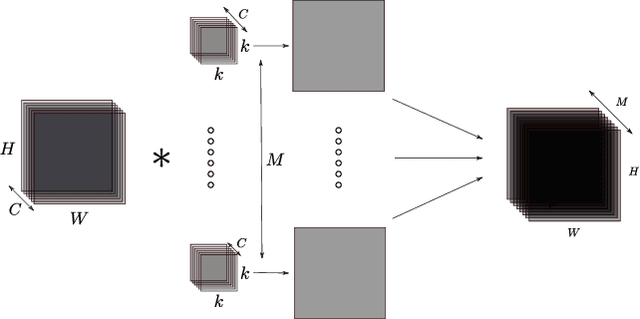
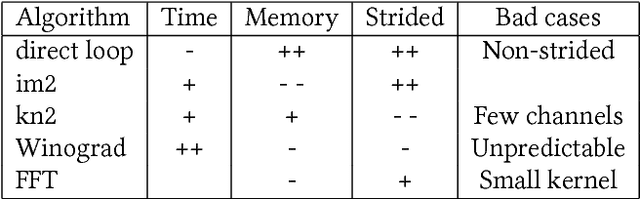
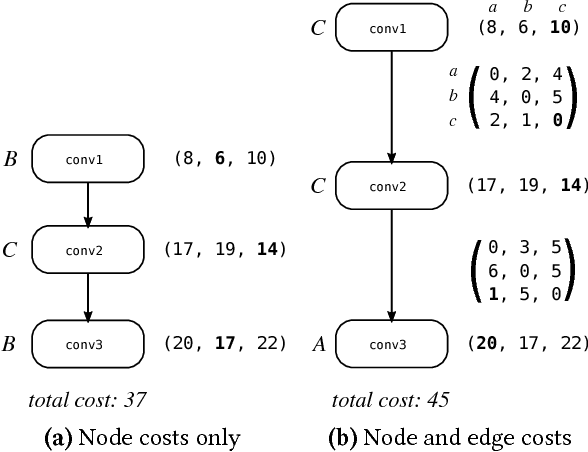
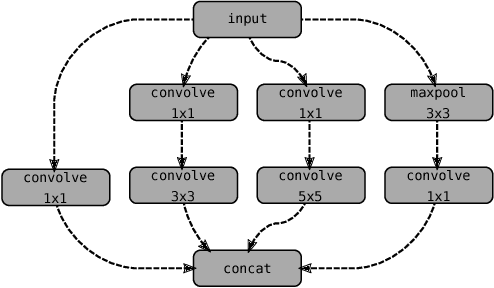
Deep Neural Networks (DNNs) require very large amounts of computation both for training and for inference when deployed in the field. Many different algorithms have been proposed to implement the most computationally expensive layers of DNNs. Further, each of these algorithms has a large number of variants, which offer different trade-offs of parallelism, data locality, memory footprint, and execution time. In addition, specific algorithms operate much more efficiently on specialized data layouts and formats. We state the problem of optimal primitive selection in the presence of data format transformations, and show that it is NP-hard by demonstrating an embedding in the Partitioned Boolean Quadratic Assignment problem (PBQP). We propose an analytic solution via a PBQP solver, and evaluate our approach experimentally by optimizing several popular DNNs using a library of more than 70 DNN primitives, on an embedded platform and a general purpose platform. We show experimentally that significant gains are possible versus the state of the art vendor libraries by using a principled analytic solution to the problem of layout selection in the presence of data format transformations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge