Optimal Clustering in Anisotropic Gaussian Mixture Models
Paper and Code
Jan 18, 2021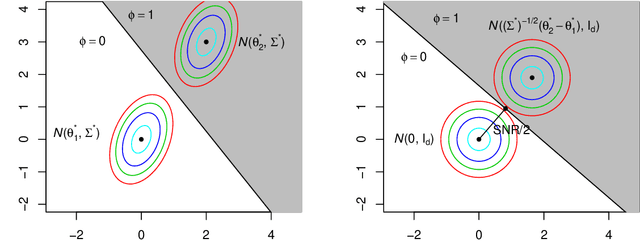
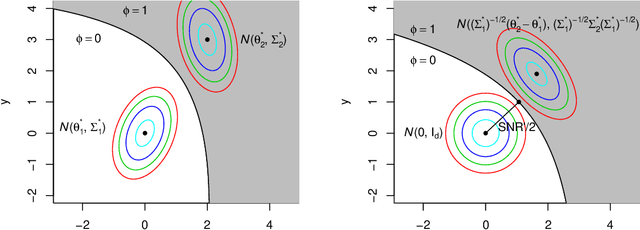
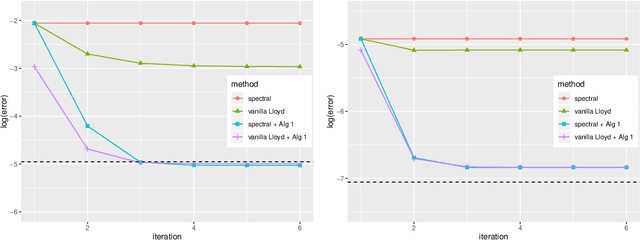
We study the clustering task under anisotropic Gaussian Mixture Models where the covariance matrices from different clusters are unknown and are not necessarily the identical matrix. We characterize the dependence of signal-to-noise ratios on the cluster centers and covariance matrices and obtain the minimax lower bound for the clustering problem. In addition, we propose a computationally feasible procedure and prove it achieves the optimal rate within a few iterations. The proposed procedure is a hard EM type algorithm, and it can also be seen as a variant of the Lloyd's algorithm that is adjusted to the anisotropic covariance matrices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge