Online Matrix Completion with Side Information
Paper and Code
Jun 17, 2019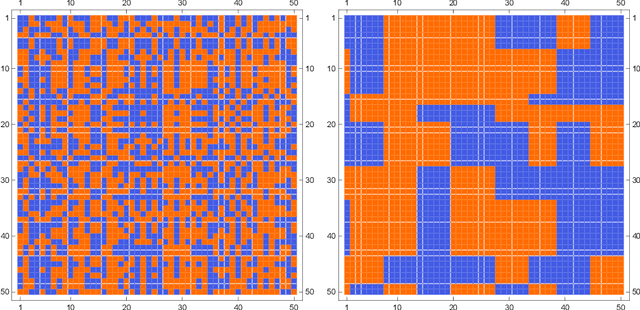
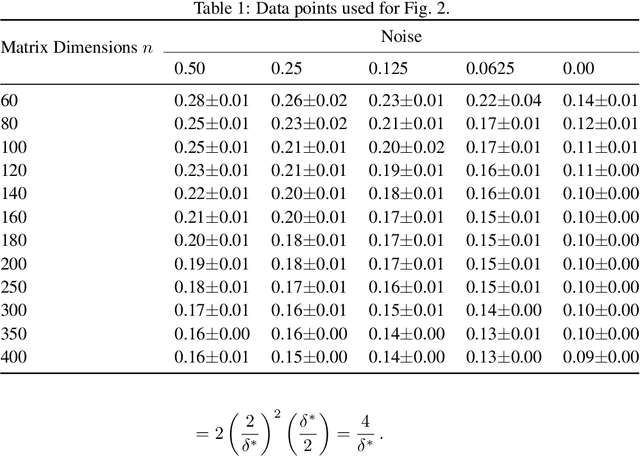
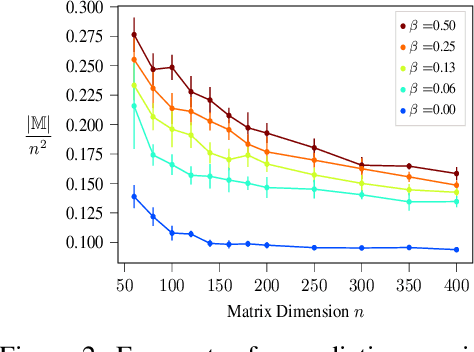
We give an online algorithm and prove novel mistake and regret bounds for online binary matrix completion with side information. The bounds we prove are of the form $\tilde{\mathcal{O}}({\mathcal{D}}/{\gamma^2})$. The term ${1}/{\gamma^2}$ is analogous to the usual margin term in SVM (perceptron) bounds. More specifically, if we assume that there is some factorization of the underlying $m\times n$ matrix into $\mathbf{P} \mathbf{Q}^{\top}$ where the rows of $\mathbf{P}$ are interpreted as ``classifiers'' in $\Re^d$ and the rows of $\mathbf{Q}$ as ``instances'' in $\Re^d$, then $\gamma$ is is the maximum (normalized) margin over all factorizations $\mathbf{P} \mathbf{Q}^{\top}$ consistent with the observed matrix. The quasi-dimension term $\mathcal{D}$ measures the quality of side information. In the presence of no side information, $\mathcal{D} = m+n$. However, if the side information is predictive of the underlying factorization of the matrix, then in the best case, $\mathcal{D} \in \mathcal{O}(k + \ell)$ where $k$ is the number of distinct row factors and $\ell$ is the number of distinct column factors. We additionally provide a generalization of our algorithm to the inductive setting. In this setting, the side information is not specified in advance. The results are similar to the transductive setting but in the best case, the quasi-dimension $\mathcal{D}$ is now bounded by $\mathcal{O}(k^2 + \ell^2)$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge