On Training Neural Networks with Mixed Integer Programming

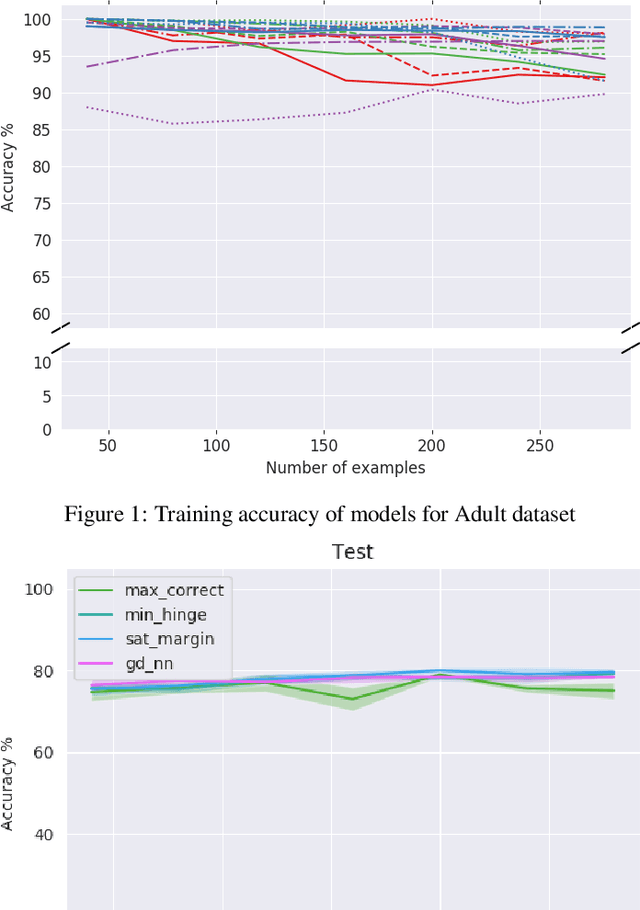
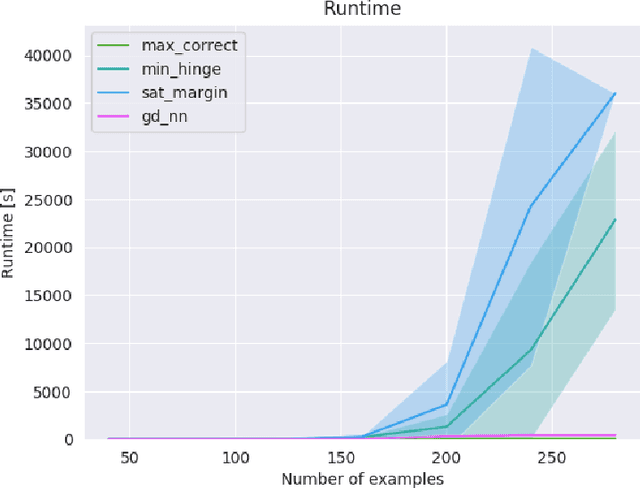
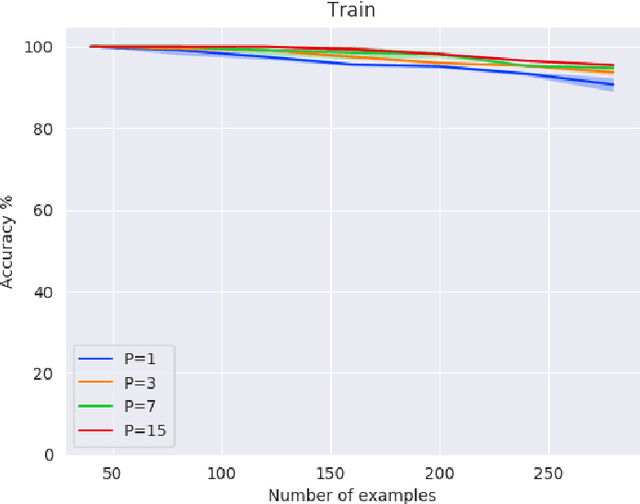
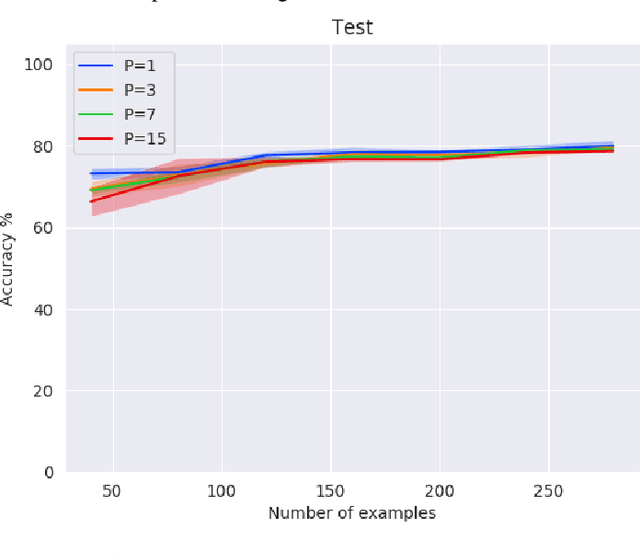
Recent work has shown potential in using Mixed Integer Programming (MIP) solvers to optimize certain aspects of neural networks (NN). However little research has gone into training NNs with solvers. State of the art methods to train NNs are typically gradient-based and require significant data, computation on GPUs and extensive hyper-parameter tuning. In contrast, training with MIP solvers should not require GPUs or hyper-parameter tuning but can likely not handle large amounts of data. This work builds on recent advances that train binarized NNs using MIP solvers. We go beyond current work by formulating new MIP models to increase the amount of data that can be used and to train non-binary integer-valued networks. Our results show that comparable results to using gradient descent can be achieved when minimal data is available.