On the Nash equilibrium of moment-matching GANs for stationary Gaussian processes
Paper and Code
Mar 14, 2022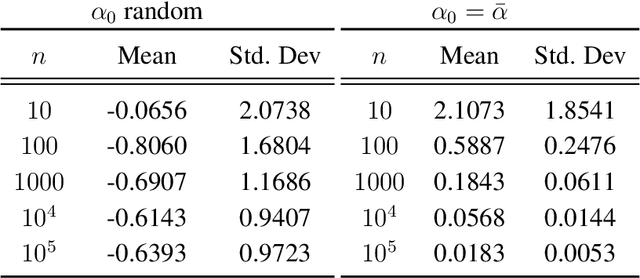
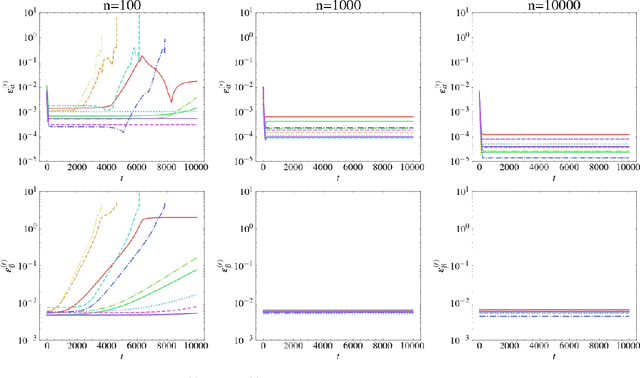
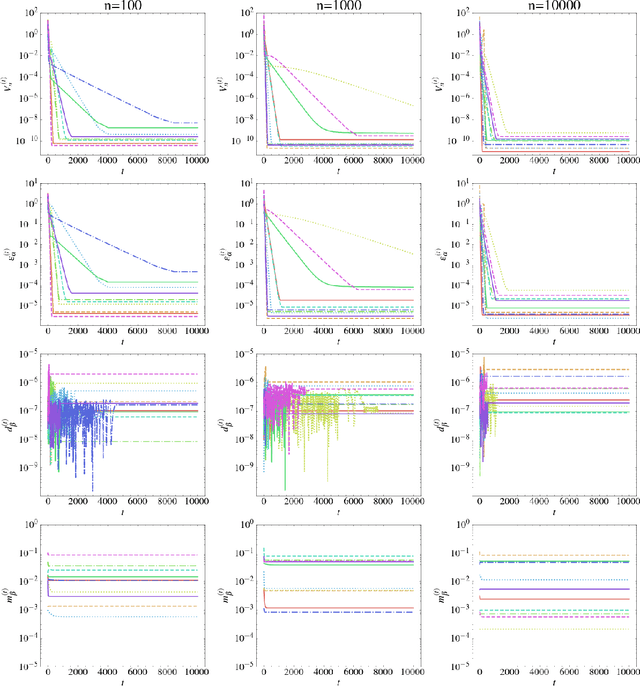
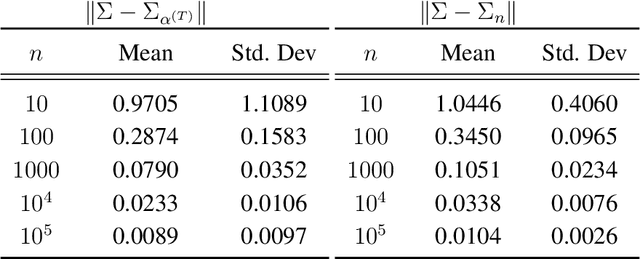
Generative Adversarial Networks (GANs) learn an implicit generative model from data samples through a two-player game. In this paper, we study the existence of Nash equilibrium of the game which is consistent as the number of data samples grows to infinity. In a realizable setting where the goal is to estimate the ground-truth generator of a stationary Gaussian process, we show that the existence of consistent Nash equilibrium depends crucially on the choice of the discriminator family. The discriminator defined from second-order statistical moments can result in non-existence of Nash equilibrium, existence of consistent non-Nash equilibrium, or existence and uniqueness of consistent Nash equilibrium, depending on whether symmetry properties of the generator family are respected. We further study the local stability and global convergence of gradient descent-ascent methods towards consistent equilibrium.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge