On the Kurtosis of Modulation Formats for Characterizing the Nonlinear Fiber Propagation
Paper and Code
Dec 07, 2021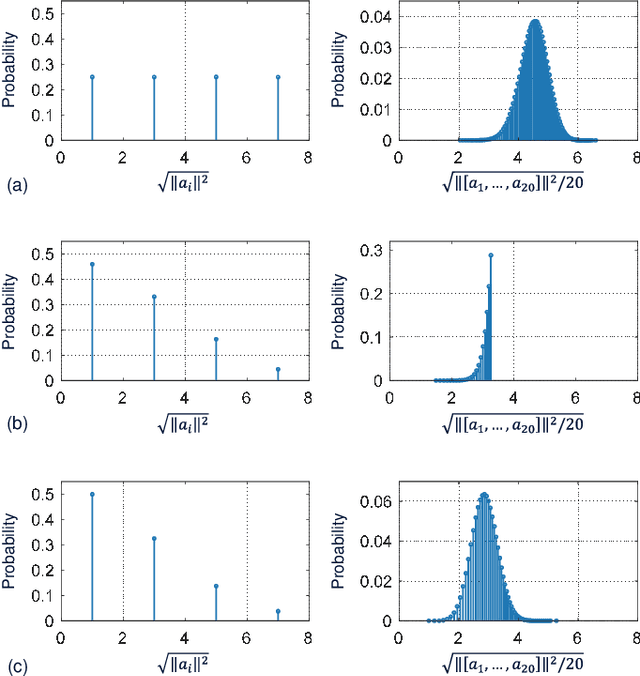
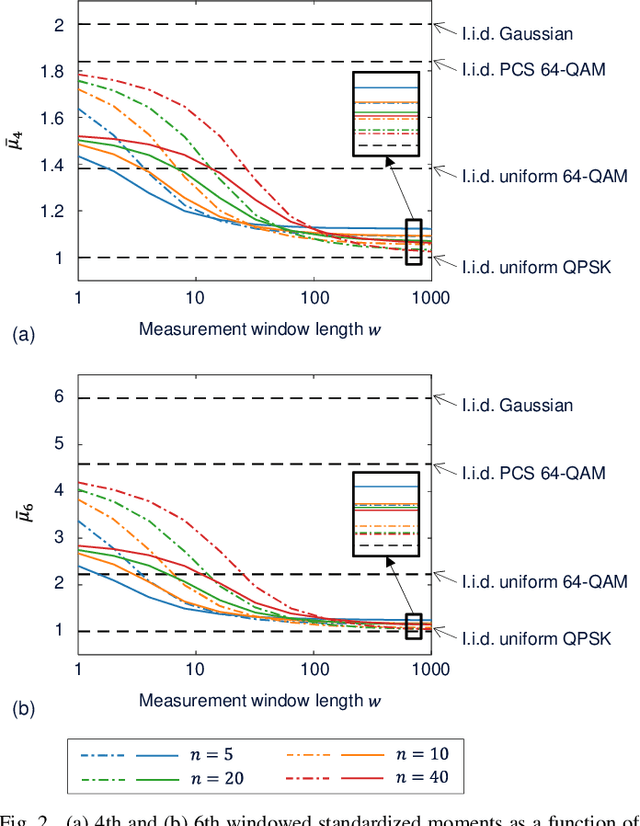
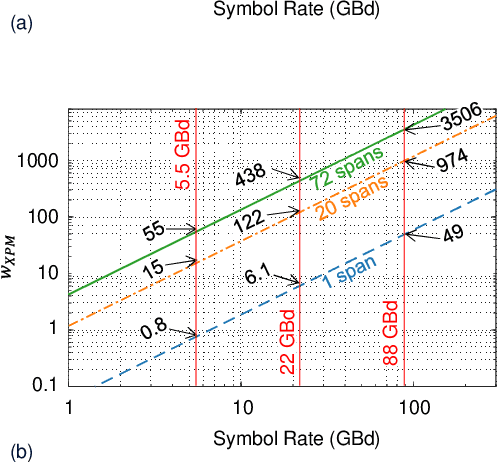
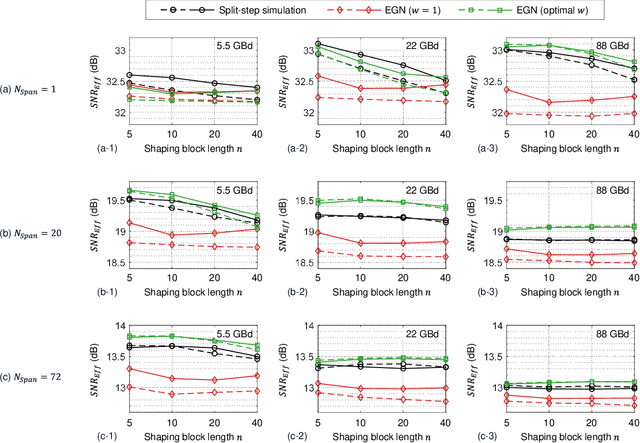
Knowing only two high-order statistical moments of modulation symbols, often represented by the fourth moment called "kurtosis", the overestimation of nonlinear interference (NLI) in a Gaussian noise (GN) model due to Gaussian signaling assumption can be corrected through an enhanced GN (EGN) model. However, in some modern optical communication systems where the transmitted modulation symbols are statistically correlated, such as in systems that use probabilistic constellation shaping (PCS) with finite-length sphere shaping, the kurtosis-based EGN model produces significant inaccuracies in analytical prediction of NLI. In this paper, we show that for correlated modulation symbols, the NLI can be more accurately estimated by substituting a statistical measure called windowed kurtosis into the EGN model, instead of the conventional kurtosis. Remarkably, the optimal window length for windowed kurtosis is found to be consistent with the self-phase modulation (SPM) and cross-phase modulation (XPM) characteristic times in various system configurations. The findings can be used in practice to analytically evaluate and design NLI-tolerant modulation formats.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge