On the Inductive Bias of a CNN for Orthogonal Patterns Distributions

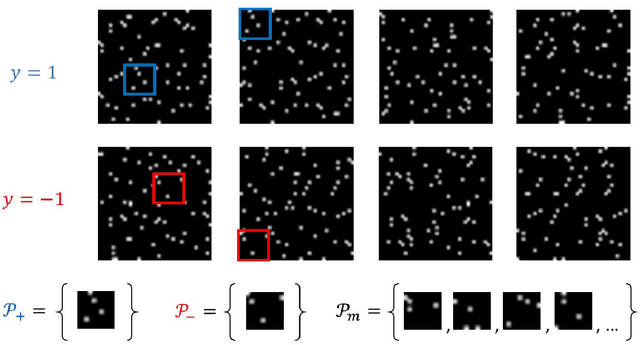
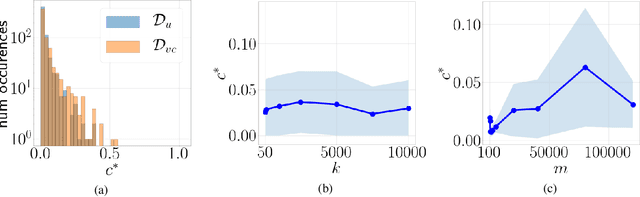
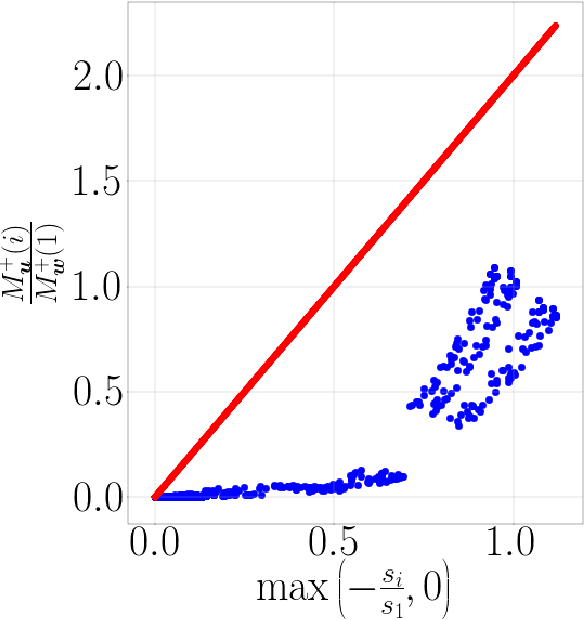
Training overparameterized convolutional neural networks with gradient based methods is the most successful learning method for image classification. However, its theoretical properties are far from understood even for very simple learning tasks. In this work, we consider a simplified image classification task where images contain orthogonal patches and are learned with a 3-layer overparameterized convolutional network and stochastic gradient descent. We empirically identify a novel phenomenon where the dot-product between the learned pattern detectors and their detected patterns are governed by the pattern statistics in the training set. We call this phenomenon Pattern Statistics Inductive Bias (PSI) and prove that PSI holds for a simple setup with two points in the training set. Furthermore, we prove that if PSI holds, stochastic gradient descent has sample complexity $O(d^2\log(d))$ where $d$ is the filter dimension. In contrast, we show a VC dimension lower bound in our setting which is exponential in $d$. Taken together, our results provide strong evidence that PSI is a unique inductive bias of stochastic gradient descent, that guarantees good generalization properties.