On the Difference Between the Information Bottleneck and the Deep Information Bottleneck
Paper and Code
Dec 31, 2019
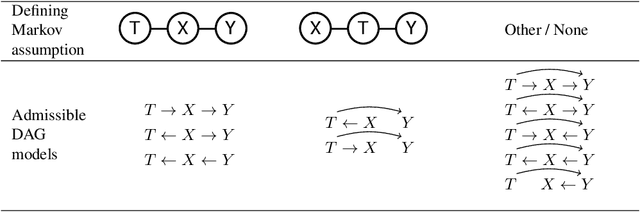
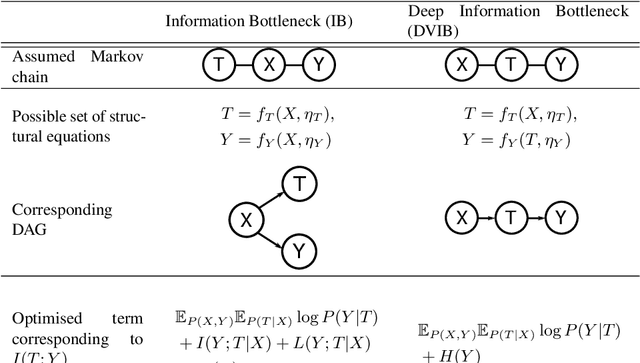
Combining the Information Bottleneck model with deep learning by replacing mutual information terms with deep neural nets has proved successful in areas ranging from generative modelling to interpreting deep neural networks. In this paper, we revisit the Deep Variational Information Bottleneck and the assumptions needed for its derivation. The two assumed properties of the data $X$, $Y$ and their latent representation $T$ take the form of two Markov chains $T-X-Y$ and $X-T-Y$. Requiring both to hold during the optimisation process can be limiting for the set of potential joint distributions $P(X,Y,T)$. We therefore show how to circumvent this limitation by optimising a lower bound for $I(T;Y)$ for which only the latter Markov chain has to be satisfied. The actual mutual information consists of the lower bound which is optimised in DVIB and cognate models in practice and of two terms measuring how much the former requirement $T-X-Y$ is violated. Finally, we propose to interpret the family of information bottleneck models as directed graphical models and show that in this framework the original and deep information bottlenecks are special cases of a fundamental IB model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge