On scale-invariant properties in natural images and their simulations

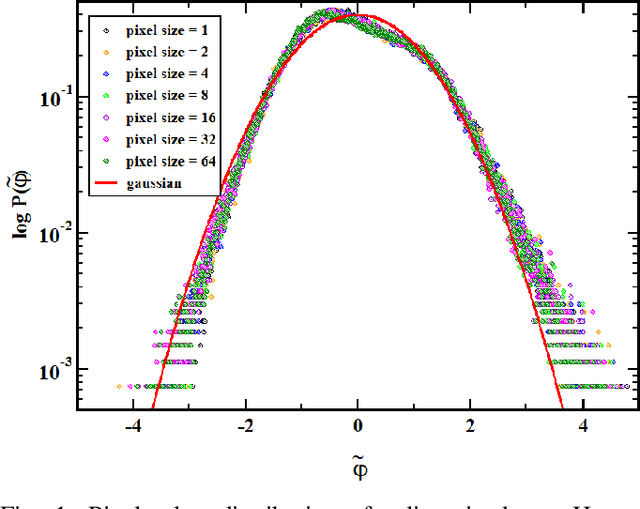
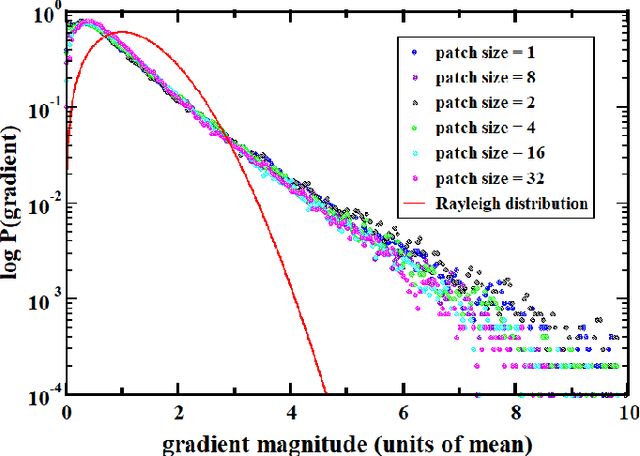
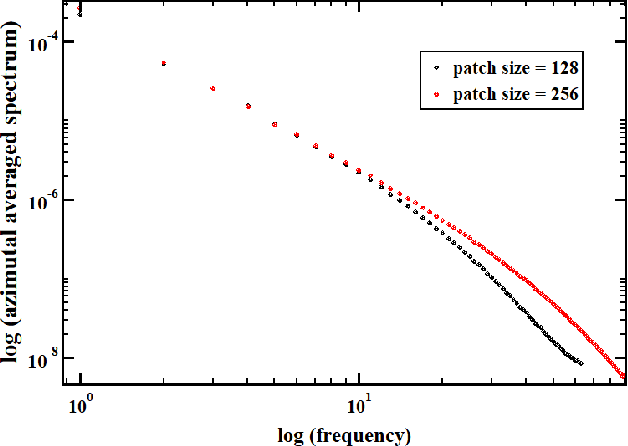
We study samples of natural images for which a set of statistical characteristics is computed and scale-invariant properties of samples are demonstrated computationally. Computations of the power spectrum are carried out and a power-law decaying power spectrum is observed on samples taken from van Hateren images of natural scenes. We propose a dynamic model to reproduce the observed slope in the power spectrum qualitatively. For two types of sources for this model the behaviour of power spectrum is investigated and scale-invariance confirmed numerically. We then discuss potential applications of scale-invariant properties of natural images.