On Convergent Finite Difference Schemes for Variational - PDE Based Image Processing
Paper and Code
Sep 16, 2013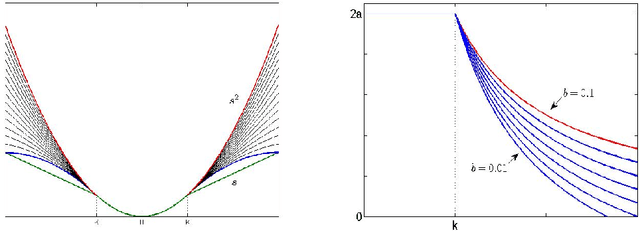
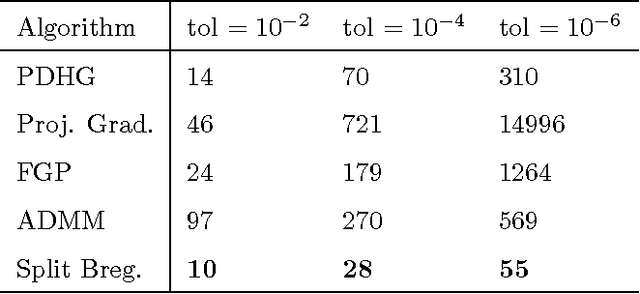

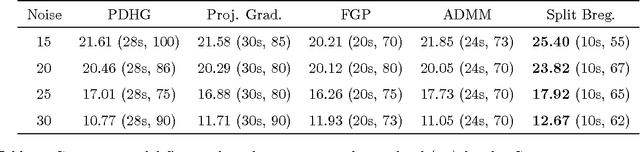
We study an adaptive anisotropic Huber functional based image restoration scheme. By using a combination of L2-L1 regularization functions, an adaptive Huber functional based energy minimization model provides denoising with edge preservation in noisy digital images. We study a convergent finite difference scheme based on continuous piecewise linear functions and use a variable splitting scheme, namely the Split Bregman, to obtain the discrete minimizer. Experimental results are given in image denoising and comparison with additive operator splitting, dual fixed point, and projected gradient schemes illustrate that the best convergence rates are obtained for our algorithm.
* Computational and Applied Mathematics, 2017 * 23 pages, 12 figures, 2 tables
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge