On a New Improvement-Based Acquisition Function for Bayesian Optimization
Paper and Code
Aug 21, 2018

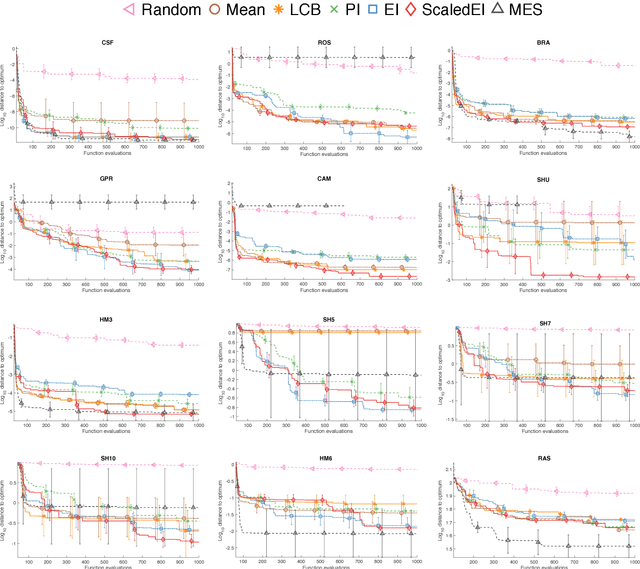
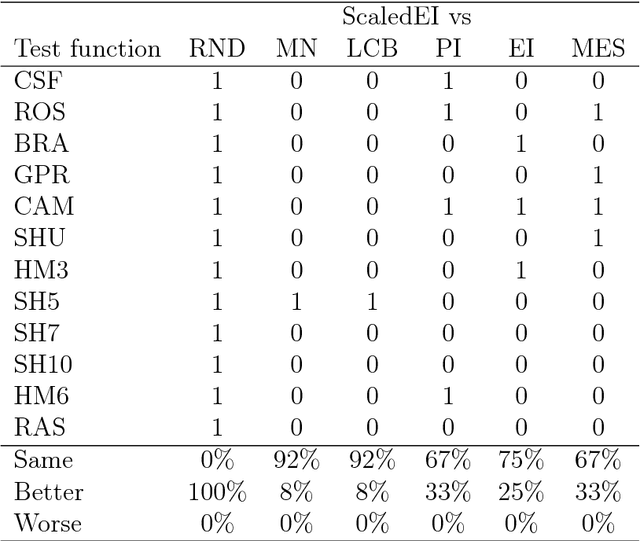
Bayesian optimization (BO) is a popular algorithm for solving challenging optimization tasks. It is designed for problems where the objective function is expensive to evaluate, perhaps not available in exact form, without gradient information and possibly returning noisy values. Different versions of the algorithm vary in the choice of the acquisition function, which recommends the point to query the objective at next. Initially, researchers focused on improvement-based acquisitions, while recently the attention has shifted to more computationally expensive information-theoretical measures. In this paper we present two major contributions to the literature. First, we propose a new improvement-based acquisition function that recommends query points where the improvement is expected to be high with high confidence. The proposed algorithm is evaluated on a large set of benchmark functions from the global optimization literature, where it turns out to perform at least as well as current state-of-the-art acquisition functions, and often better. This suggests that it is a powerful default choice for BO. The novel policy is then compared to widely used global optimization solvers in order to confirm that BO methods reduce the computational costs of the optimization by keeping the number of function evaluations small. The second main contribution represents an application to precision medicine, where the interest lies in the estimation of parameters of a partial differential equations model of the human pulmonary blood circulation system. Once inferred, these parameters can help clinicians in diagnosing a patient with pulmonary hypertension without going through the standard invasive procedure of right heart catheterization, which can lead to side effects and complications (e.g. severe pain, internal bleeding, thrombosis).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge