Of the People: Voting Is More Effective with Representative Candidates
Paper and Code
Aug 26, 2017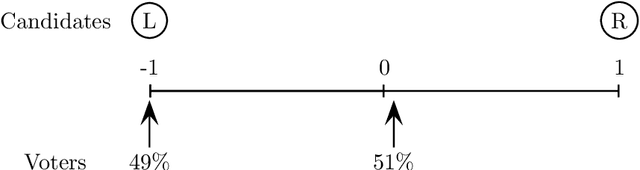

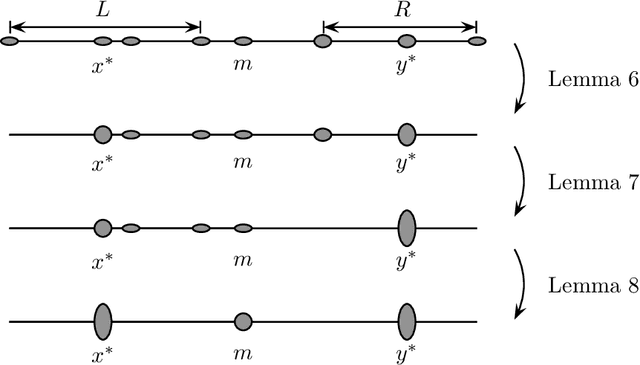
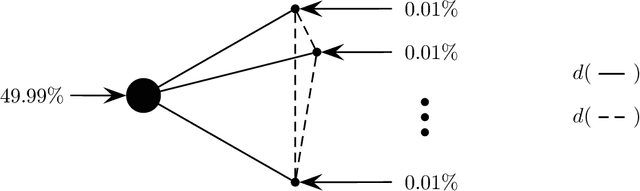
In light of the classic impossibility results of Arrow and Gibbard and Satterthwaite regarding voting with ordinal rules, there has been recent interest in characterizing how well common voting rules approximate the social optimum. In order to quantify the quality of approximation, it is natural to consider the candidates and voters as embedded within a common metric space, and to ask how much further the chosen candidate is from the population as compared to the socially optimal one. We use this metric preference model to explore a fundamental and timely question: does the social welfare of a population improve when candidates are representative of the population? If so, then by how much, and how does the answer depend on the complexity of the metric space? We restrict attention to the most fundamental and common social choice setting: a population of voters, two independently drawn candidates, and a majority rule election. When candidates are not representative of the population, it is known that the candidate selected by the majority rule can be thrice as far from the population as the socially optimal one. We examine how this ratio improves when candidates are drawn independently from the population of voters. Our results are two-fold: When the metric is a line, the ratio improves from $3$ to $4-2\sqrt{2}$, roughly $1.1716$; this bound is tight. When the metric is arbitrary, we show a lower bound of $1.5$ and a constant upper bound strictly better than $2$ on the approximation ratio of the majority rule. The positive result depends in part on the assumption that candidates are independent and identically distributed. However, we show that independence alone is not enough to achieve the upper bound: even when candidates are drawn independently, if the population of candidates can be different from the voters, then an upper bound of $2$ on the approximation is tight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge