Number Sequence Prediction Problems and Computational Powers of Neural Network Models

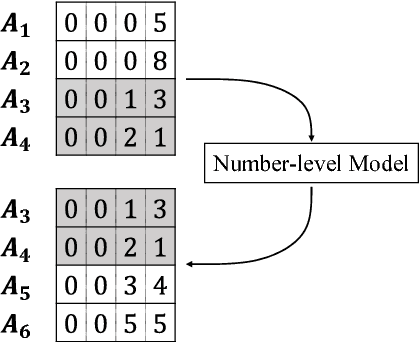
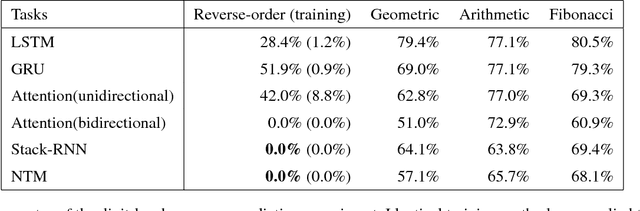
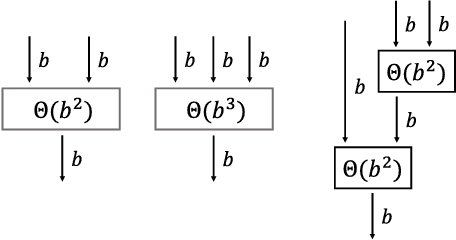
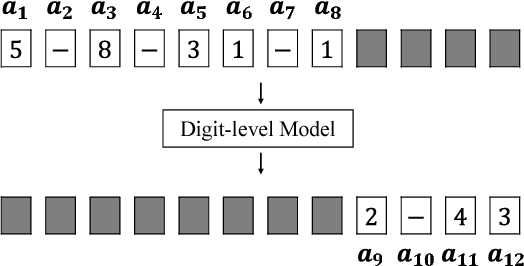
Inspired by number series tests to measure human intelligence, we suggest number sequence prediction tasks to assess neural network models' computational powers for solving algorithmic problems. We define complexity and difficulty of a number sequence prediction task with the structure of the smallest automation that can generate the sequence. We suggest two types of number sequence prediction problems: the number-level and the digit-level problems. The number-level problems format sequences as 2-dimensional grids of digits, and the digit-level problem provides a single digit input per a time step, hence solving this problem is equivalent to modeling a sequential state automation. The complexity of a number-level sequence problem can be defined with the depth of an equivalent combinatorial logic. Experimental results with CNN models suggest that they are capable of learning the compound operations of the number-level sequence generation rules but the depths of the compound operations are limited. For the digit-level problems, GRU and LSTM models can solve the problems with complexity of finite state automations, but they cannot solve the problems with complexity of pushdown automations or Turing machines. The results show that our number sequence prediction problems effectively evaluate machine learning models' computational capabilities.