Neural Wave Functions for Superfluids

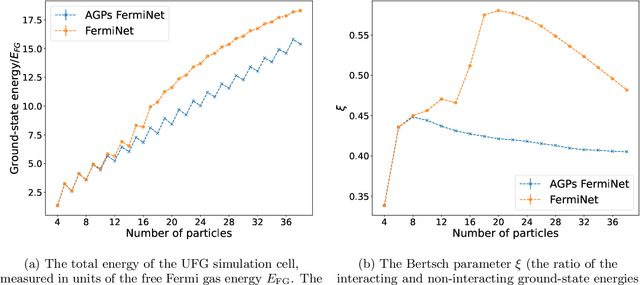
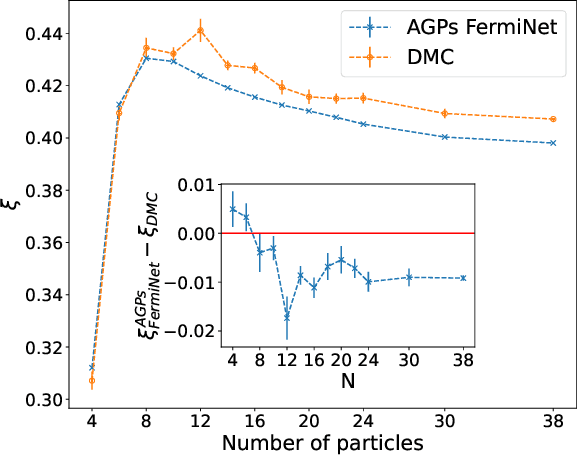
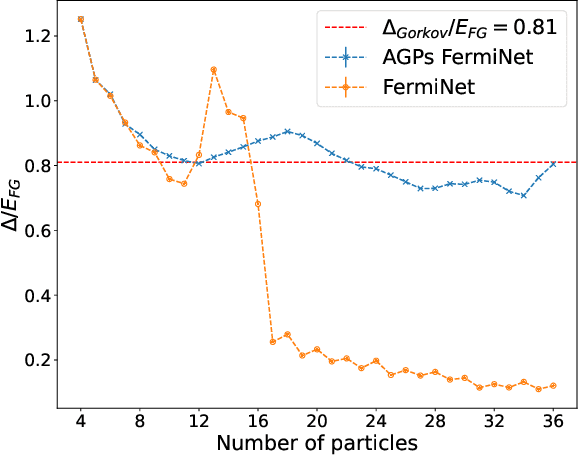
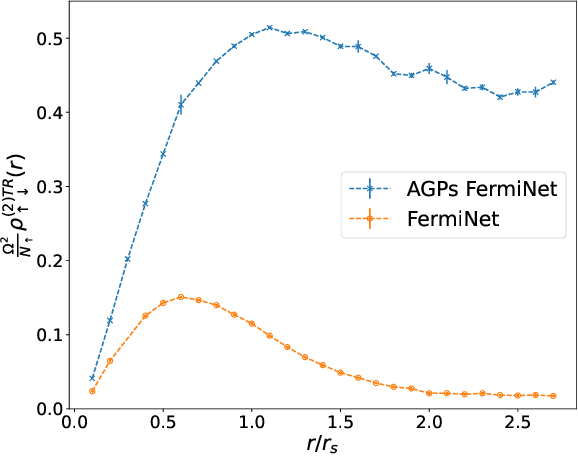
Understanding superfluidity remains a major goal of condensed matter physics. Here we tackle this challenge utilizing the recently developed Fermionic neural network (FermiNet) wave function Ansatz for variational Monte Carlo calculations. We study the unitary Fermi gas, a system with strong, short-range, two-body interactions known to possess a superfluid ground state but difficult to describe quantitively. We demonstrate key limitations of the FermiNet Ansatz in studying the unitary Fermi gas and propose a simple modification that outperforms the original FermiNet significantly, giving highly accurate results. We prove mathematically that the new Ansatz is a strict generalization of the original FermiNet architecture, despite the use of fewer parameters. Our approach shares several advantanges with the FermiNet: the use of a neural network removes the need for an underlying basis set; and the flexiblity of the network yields extremely accurate results within a variational quantum Monte Carlo framework that provides access to unbiased estimates of arbitrary ground-state expectation values. We discuss how the method can be extended to study other superfluids.