Neural Hilbert Ladders: Multi-Layer Neural Networks in Function Space
Paper and Code
Jul 03, 2023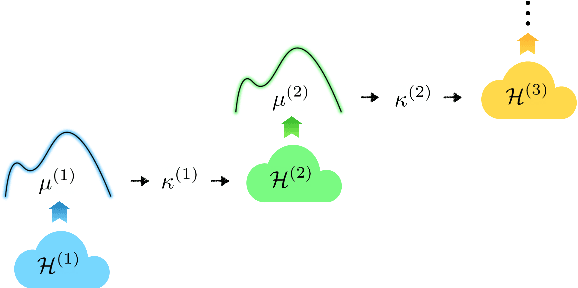
The characterization of the functions spaces explored by neural networks (NNs) is an important aspect of deep learning theory. In this work, we view a multi-layer NN with arbitrary width as defining a particular hierarchy of reproducing kernel Hilbert spaces (RKHSs), named a Neural Hilbert Ladder (NHL). This allows us to define a function space and a complexity measure that generalize prior results for shallow NNs, and we then examine their theoretical properties and implications in several aspects. First, we prove a correspondence between functions expressed by L-layer NNs and those belonging to L-level NHLs. Second, we prove generalization guarantees for learning an NHL with the complexity measure controlled. Third, corresponding to the training of multi-layer NNs in the infinite-width mean-field limit, we derive an evolution of the NHL characterized as the dynamics of multiple random fields. Fourth, we show examples of depth separation in NHLs under ReLU and quadratic activation functions. Finally, we complement the theory with numerical results to illustrate the learning of RKHS in NN training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge