Network Detection Theory and Performance
Paper and Code
Mar 22, 2013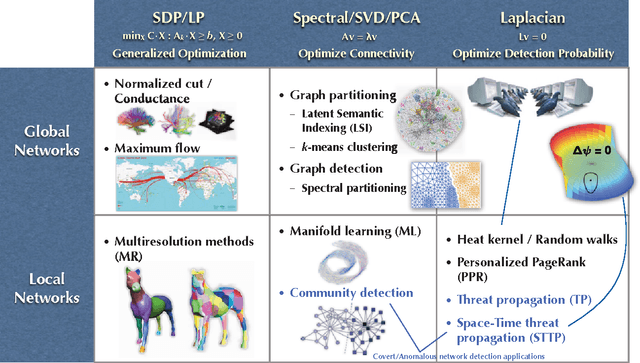
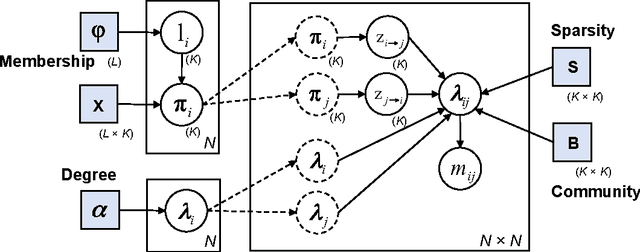
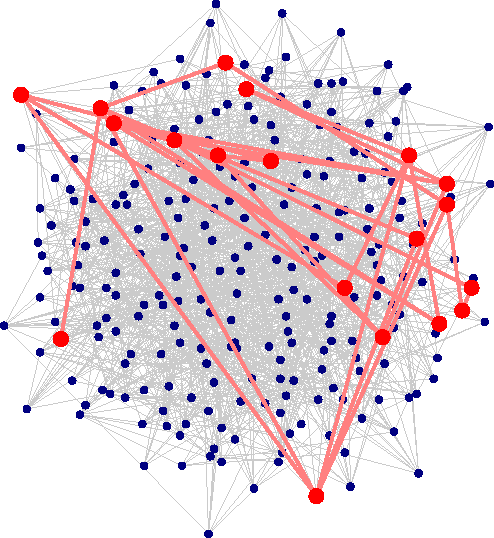
Network detection is an important capability in many areas of applied research in which data can be represented as a graph of entities and relationships. Oftentimes the object of interest is a relatively small subgraph in an enormous, potentially uninteresting background. This aspect characterizes network detection as a "big data" problem. Graph partitioning and network discovery have been major research areas over the last ten years, driven by interest in internet search, cyber security, social networks, and criminal or terrorist activities. The specific problem of network discovery is addressed as a special case of graph partitioning in which membership in a small subgraph of interest must be determined. Algebraic graph theory is used as the basis to analyze and compare different network detection methods. A new Bayesian network detection framework is introduced that partitions the graph based on prior information and direct observations. The new approach, called space-time threat propagation, is proved to maximize the probability of detection and is therefore optimum in the Neyman-Pearson sense. This optimality criterion is compared to spectral community detection approaches which divide the global graph into subsets or communities with optimal connectivity properties. We also explore a new generative stochastic model for covert networks and analyze using receiver operating characteristics the detection performance of both classes of optimal detection techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge