N-grams Bayesian Differential Privacy
Paper and Code
Jan 29, 2021
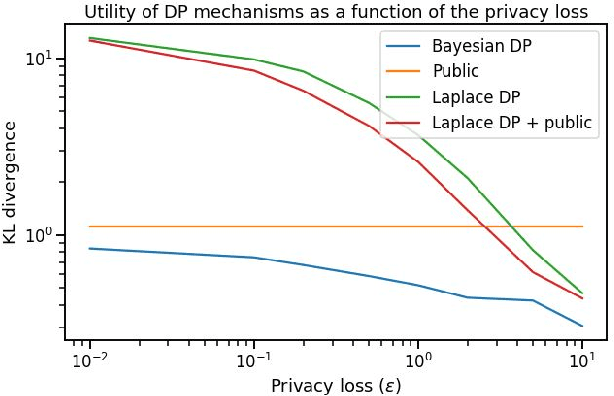
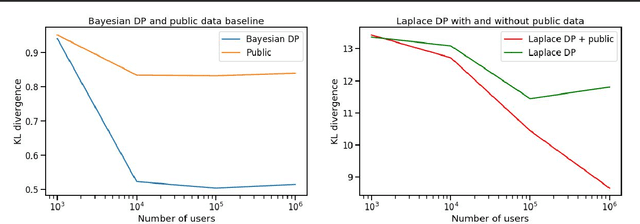
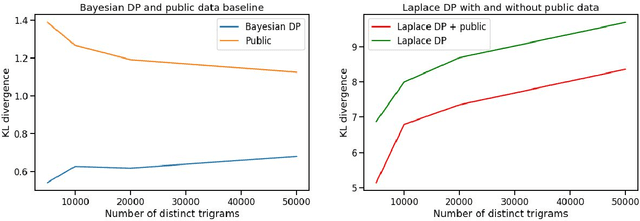
Differential privacy has gained popularity in machine learning as a strong privacy guarantee, in contrast to privacy mitigation techniques such as k-anonymity. However, applying differential privacy to n-gram counts significantly degrades the utility of derived language models due to their large vocabularies. We propose a differential privacy mechanism that uses public data as a prior in a Bayesian setup to provide tighter bounds on the privacy loss metric epsilon, and thus better privacy-utility trade-offs. It first transforms the counts to log space, approximating the distribution of the public and private data as Gaussian. The posterior distribution is then evaluated and softmax is applied to produce a probability distribution. This technique achieves up to 85% reduction in KL divergence compared to previously known mechanisms at epsilon equals 0.1. We compare our mechanism to k-anonymity in a n-gram language modelling task and show that it offers competitive performance at large vocabulary sizes, while also providing superior privacy protection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge