Multimeasurement Generative Models

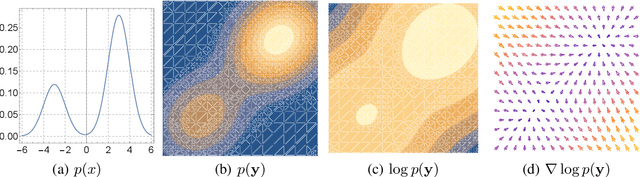
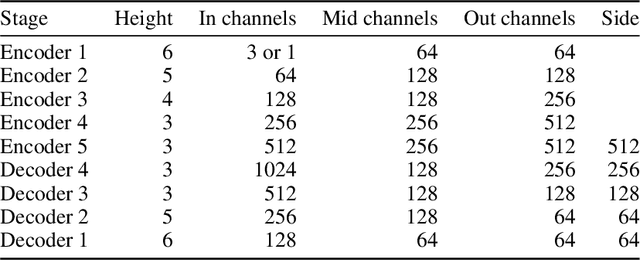
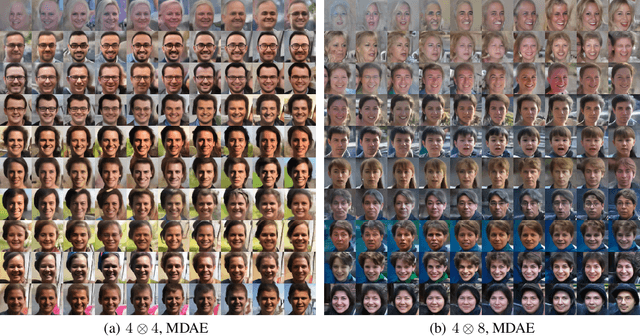
We formally map the problem of sampling from an unknown distribution with density $p_X$ in $\mathbb{R}^d$ to the problem of learning and sampling $p_\mathbf{Y}$ in $\mathbb{R}^{Md}$ obtained by convolving $p_X$ with a fixed factorial kernel: $p_\mathbf{Y}$ is referred to as M-density and the factorial kernel as multimeasurement noise model (MNM). The M-density is smoother than $p_X$, easier to learn and sample from, yet for large $M$ the two problems are mathematically equivalent since $X$ can be estimated exactly given $\mathbf{Y}=\mathbf{y}$ using the Bayes estimator $\widehat{x}(\mathbf{y})=\mathbb{E}[X\vert\mathbf{Y}=\mathbf{y}]$. To formulate the problem, we derive $\widehat{x}(\mathbf{y})$ for Poisson and Gaussian MNMs expressed in closed form in terms of unnormalized $p_\mathbf{Y}$. This leads to a simple least-squares objective for learning parametric energy and score functions. We present various parametrization schemes of interest, including one in which studying Gaussian M-densities directly leads to multidenoising autoencoders--this is the first theoretical connection made between denoising autoencoders and empirical Bayes in the literature. Samples from $p_X$ are obtained by walk-jump sampling (Saremi & Hyvarinen, 2019) via underdamped Langevin MCMC (walk) to sample from $p_\mathbf{Y}$ and the multimeasurement Bayes estimation of $X$ (jump). We study permutation invariant Gaussian M-densities on MNIST, CIFAR-10, and FFHQ-256 datasets, and demonstrate the effectiveness of this framework for realizing fast-mixing stable Markov chains in high dimensions.