Multiattribute Auctions Based on Generalized Additive Independence
Paper and Code
Jan 16, 2014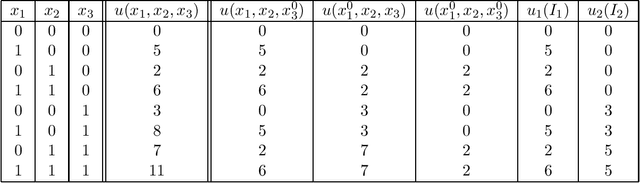



We develop multiattribute auctions that accommodate generalized additive independent (GAI) preferences. We propose an iterative auction mechanism that maintains prices on potentially overlapping GAI clusters of attributes, thus decreases elicitation and computational burden, and creates an open competition among suppliers over a multidimensional domain. Most significantly, the auction is guaranteed to achieve surplus which approximates optimal welfare up to a small additive factor, under reasonable equilibrium strategies of traders. The main departure of GAI auctions from previous literature is to accommodate non-additive trader preferences, hence allowing traders to condition their evaluation of specific attributes on the value of other attributes. At the same time, the GAI structure supports a compact representation of prices, enabling a tractable auction process. We perform a simulation study, demonstrating and quantifying the significant efficiency advantage of more expressive preference modeling. We draw random GAI-structured utility functions with various internal structures, generate additive functions that approximate the GAI utility, and compare the performance of the auctions using the two representations. We find that allowing traders to express existing dependencies among attributes improves the economic efficiency of multiattribute auctions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge