Multi-Objective Evolutionary Framework for Non-linear System Identification: A Comprehensive Investigation
Paper and Code
Aug 17, 2019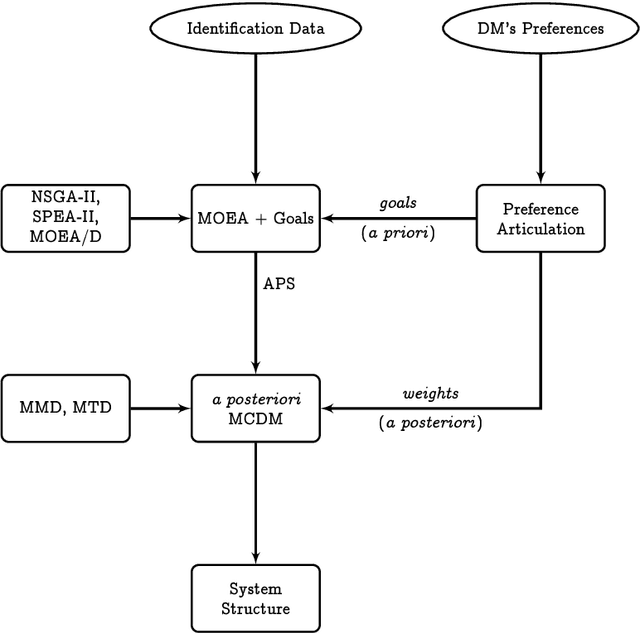

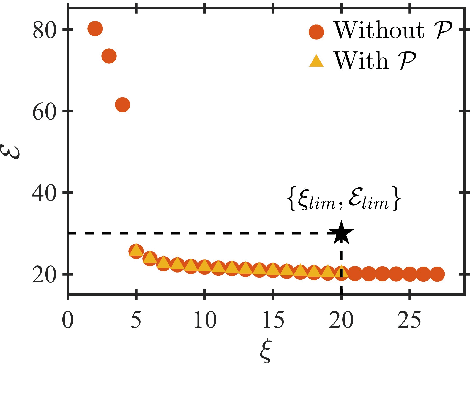
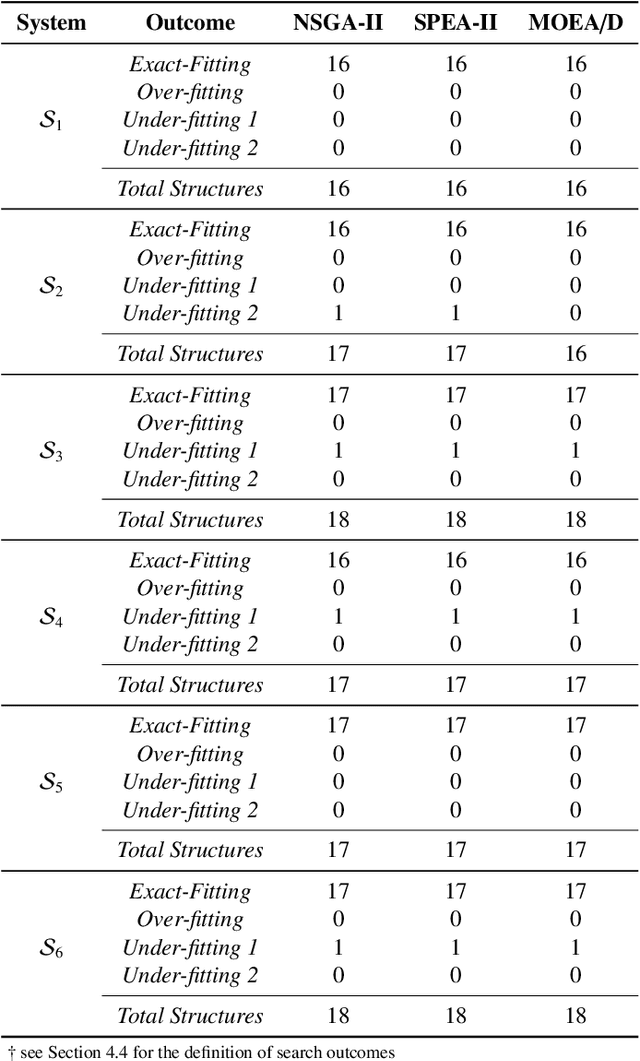
The present study proposes a multi-objective framework for structure selection of nonlinear systems which are represented by polynomial NARX models. This framework integrates the key components of Multi-Criteria Decision Making (MCDM) which include preference handling, Multi-Objective Evolutionary Algorithms (MOEAs) and a posteriori selection. To this end, three well-known MOEAs such as NSGA-II, SPEA-II and MOEA/D are thoroughly investigated to determine if there exists any significant difference in their search performance. The sensitivity of all these MOEAs to various qualitative and quantitative parameters, such as the choice of recombination mechanism, crossover and mutation probabilities, is also studied. These issues are critically analyzed considering seven discrete-time and a continuous-time benchmark nonlinear system as well as a practical case study of non-linear wave-force modeling. The results of this investigation demonstrate that MOEAs can be tailored to determine the correct structure of nonlinear systems. Further, it has been established through frequency domain analysis that it is possible to identify multiple valid discrete-time models for continuous-time systems. A rigorous statistical analysis of MOEAs via performance sweet spots in the parameter space convincingly demonstrates that these algorithms are robust over a wide range of control parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge