Multi-Access Communications with Energy Harvesting: A Multi-Armed Bandit Model and the Optimality of the Myopic Policy
Paper and Code
Jan 01, 2015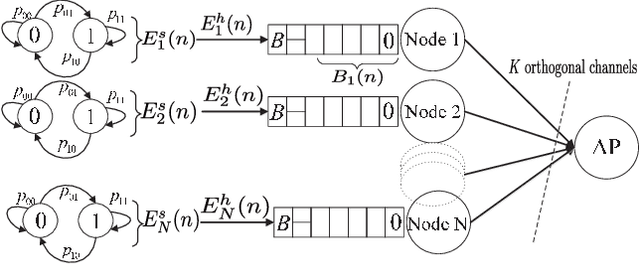
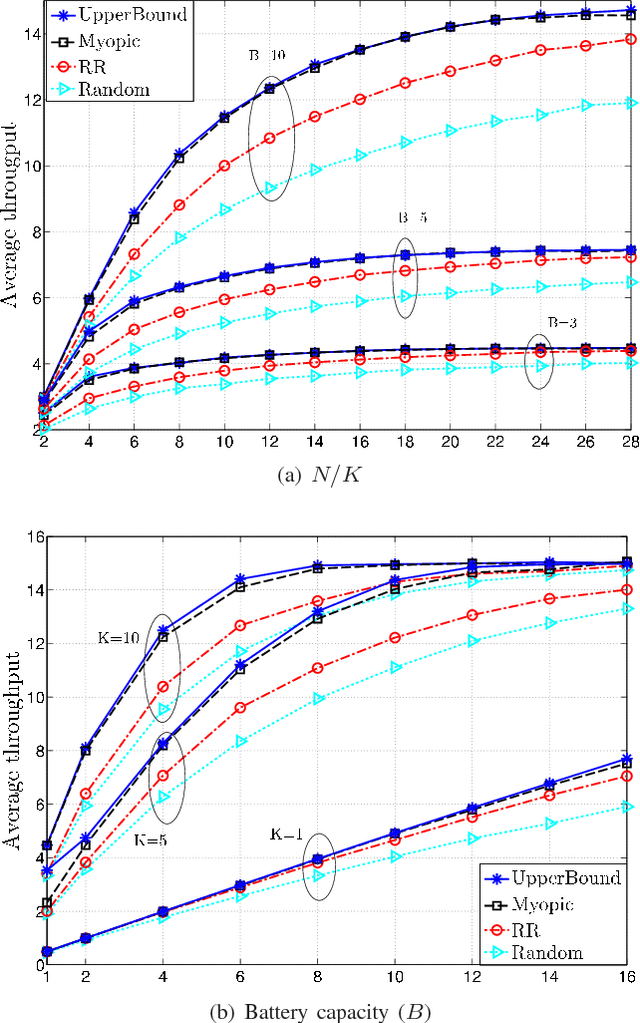
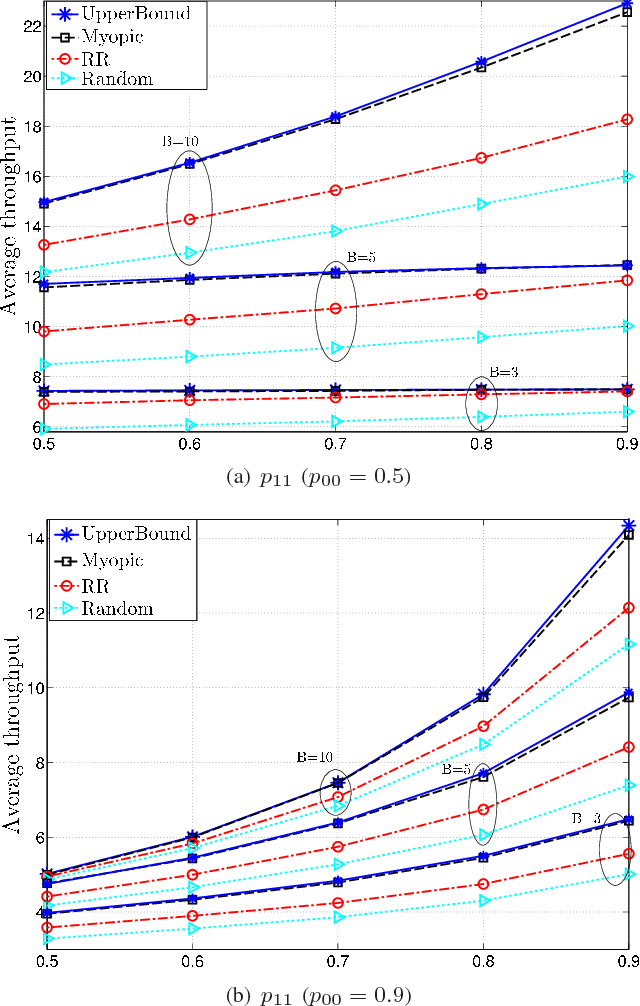
A multi-access wireless network with N transmitting nodes, each equipped with an energy harvesting (EH) device and a rechargeable battery of finite capacity, is studied. At each time slot (TS) a node is operative with a certain probability, which may depend on the availability of data, or the state of its channel. The energy arrival process at each node is modelled as an independent two-state Markov process, such that, at each TS, a node either harvests one unit of energy, or none. At each TS a subset of the nodes is scheduled by the access point (AP). The scheduling policy that maximises the total throughput is studied assuming that the AP does not know the states of either the EH processes or the batteries. The problem is identified as a restless multiarmed bandit (RMAB) problem, and an upper bound on the optimal scheduling policy is found. Under certain assumptions regarding the EH processes and the battery sizes, the optimality of the myopic policy (MP) is proven. For the general case, the performance of MP is compared numerically to the upper bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge