Model Comparison in Approximate Bayesian Computation
Paper and Code
Mar 15, 2022
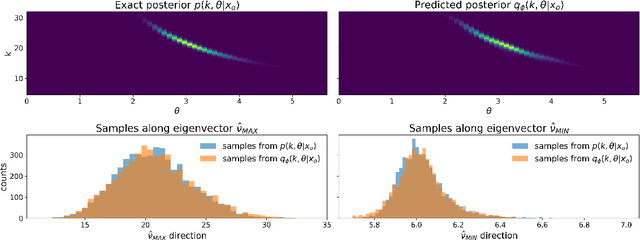


A common problem in natural sciences is the comparison of competing models in the light of observed data. Bayesian model comparison provides a statistically sound framework for this comparison based on the evidence each model provides for the data. However, this framework relies on the calculation of likelihood functions which are intractable for most models used in practice. Previous approaches in the field of Approximate Bayesian Computation (ABC) circumvent the evaluation of the likelihood and estimate the model evidence based on rejection sampling, but they are typically computationally intense. Here, I propose a new efficient method to perform Bayesian model comparison in ABC. Based on recent advances in posterior density estimation, the method approximates the posterior over models in parametric form. In particular, I train a mixture-density network to map features of the observed data to the posterior probability of the models. The performance is assessed with two examples. On a tractable model comparison problem, the underlying exact posterior probabilities are predicted accurately. In a use-case scenario from computational neuroscience -- the comparison between two ion channel models -- the underlying ground-truth model is reliably assigned a high posterior probability. Overall, the method provides a new efficient way to perform Bayesian model comparison on complex biophysical models independent of the model architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge