Mixed-Precision Inference Quantization: Radically Towards Faster inference speed, Lower Storage requirement, and Lower Loss
Paper and Code
Jul 20, 2022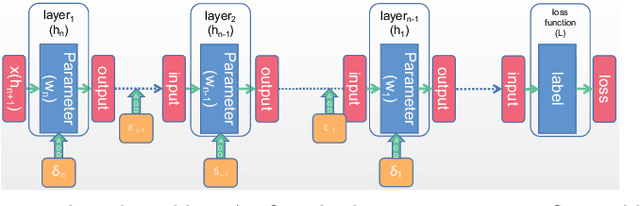
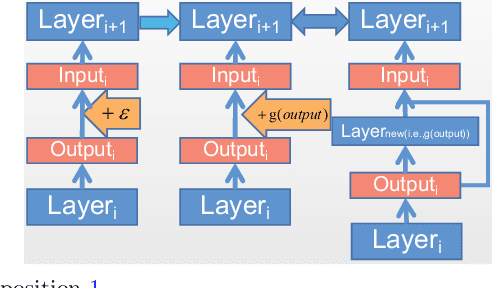
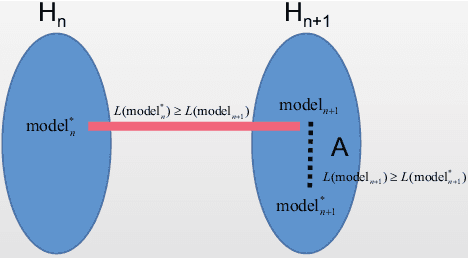
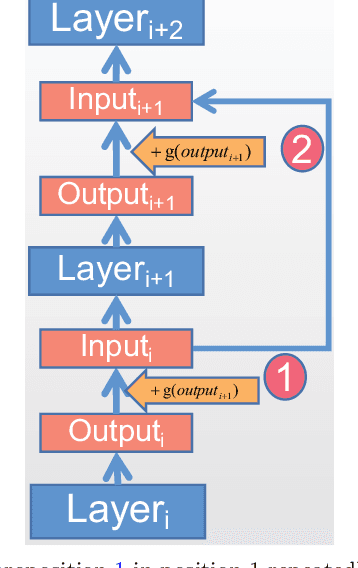
Based on the model's resilience to computational noise, model quantization is important for compressing models and improving computing speed. Existing quantization techniques rely heavily on experience and "fine-tuning" skills. In the majority of instances, the quantization model has a larger loss than a full precision model. This study provides a methodology for acquiring a mixed-precise quantization model with a lower loss than the full precision model. In addition, the analysis demonstrates that, throughout the inference process, the loss function is mostly affected by the noise of the layer inputs. In particular, we will demonstrate that neural networks with massive identity mappings are resistant to the quantization method. It is also difficult to improve the performance of these networks using quantization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge