MetaGFN: Exploring Distant Modes with Adapted Metadynamics for Continuous GFlowNets
Paper and Code
Aug 28, 2024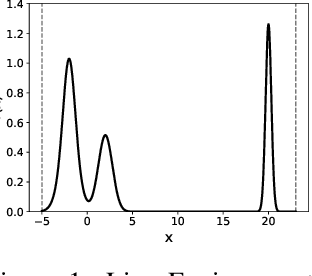
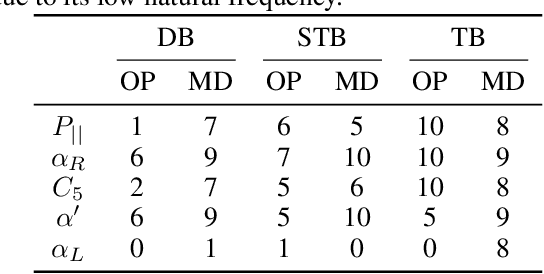
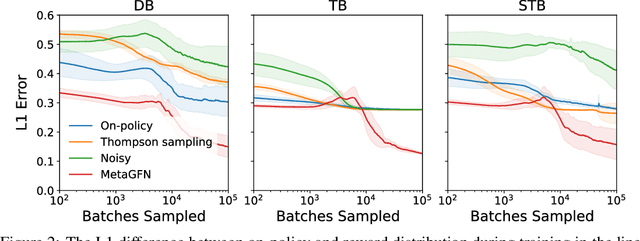
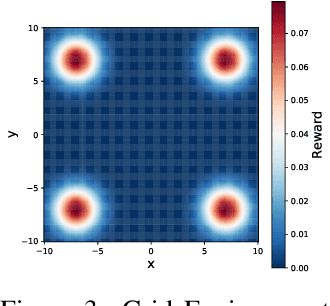
Generative Flow Networks (GFlowNets) are a class of generative models that sample objects in proportion to a specified reward function through a learned policy. They can be trained either on-policy or off-policy, needing a balance between exploration and exploitation for fast convergence to a target distribution. While exploration strategies for discrete GFlowNets have been studied, exploration in the continuous case remains to be investigated, despite the potential for novel exploration algorithms due to the local connectedness of continuous domains. Here, we introduce Adapted Metadynamics, a variant of metadynamics that can be applied to arbitrary black-box reward functions on continuous domains. We use Adapted Metadynamics as an exploration strategy for continuous GFlowNets. We show three continuous domains where the resulting algorithm, MetaGFN, accelerates convergence to the target distribution and discovers more distant reward modes than previous off-policy exploration strategies used for GFlowNets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge