Maximum n-times Coverage for COVID-19 Vaccine Design
Paper and Code
Jan 24, 2021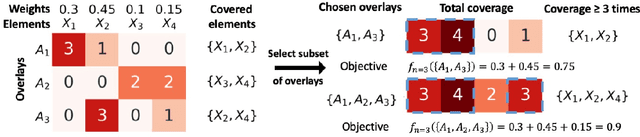

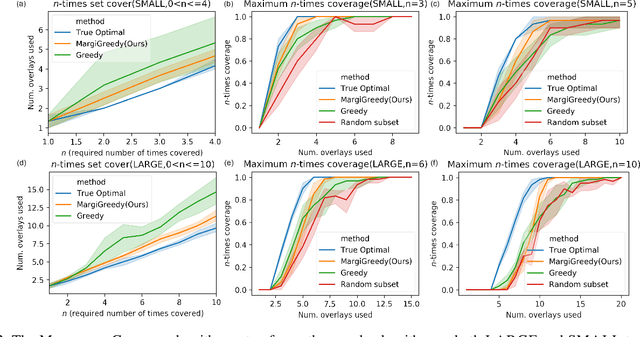
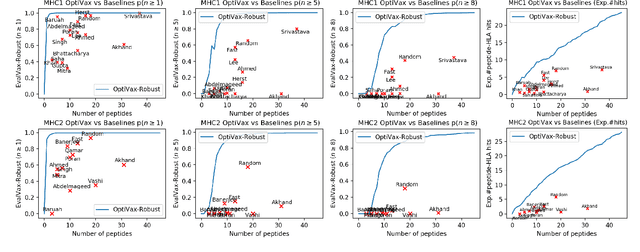
In the maximum $n$-times coverage problem, we are provided a set of elements, a weight for each element, and a set of overlays where each overlay specifies an element specific coverage of zero or more times. The goal is to select up to $k$ overlays such that the sum of the weights of elements that are covered at least $n$ times is maximized. We also define the min-cost $n$-times coverage problem where the objective is to select the minimum set of overlays such that the sum of the weights of elements that are covered at least $n$ times is at least $\tau$. We show that the $n$-times coverage objective is not submodular, and we present an efficient solution by sequential greedy optimization. We frame the design of a peptide vaccine for COVID-19 as maximum $n$-times coverage using machine learning defined candidate peptide sets, and show that our solution is superior to 29 other published COVID-19 peptide vaccine designs in predicted population coverage and the expected number of peptides displayed by each individual's HLA molecules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge