Max-Margin Stacking and Sparse Regularization for Linear Classifier Combination and Selection
Paper and Code
Jun 08, 2011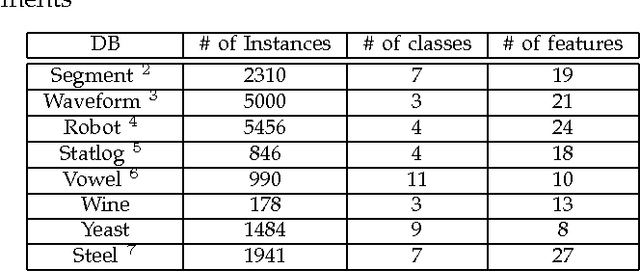

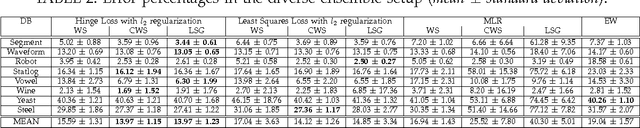

The main principle of stacked generalization (or Stacking) is using a second-level generalizer to combine the outputs of base classifiers in an ensemble. In this paper, we investigate different combination types under the stacking framework; namely weighted sum (WS), class-dependent weighted sum (CWS) and linear stacked generalization (LSG). For learning the weights, we propose using regularized empirical risk minimization with the hinge loss. In addition, we propose using group sparsity for regularization to facilitate classifier selection. We performed experiments using two different ensemble setups with differing diversities on 8 real-world datasets. Results show the power of regularized learning with the hinge loss function. Using sparse regularization, we are able to reduce the number of selected classifiers of the diverse ensemble without sacrificing accuracy. With the non-diverse ensembles, we even gain accuracy on average by using sparse regularization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge