Low Complexity Regularized Phase Retrieval

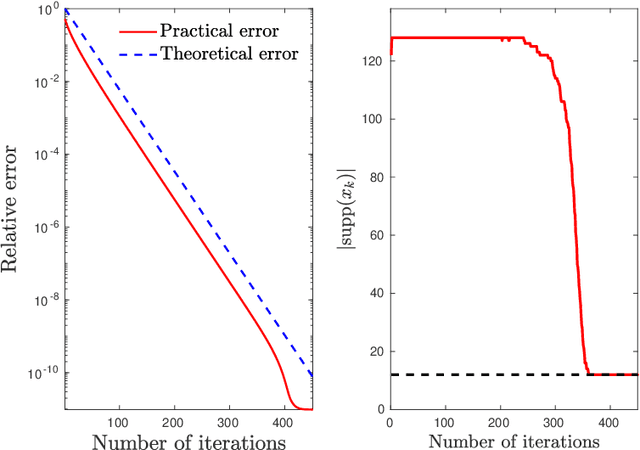
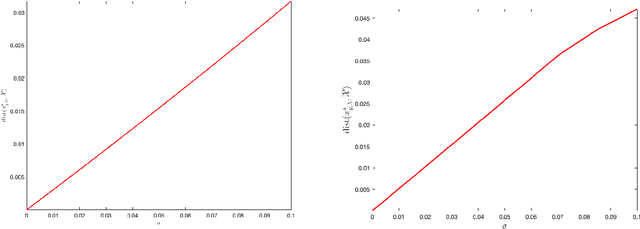
In this paper, we study the phase retrieval problem in the situation where the vector to be recovered has an a priori structure that can encoded into a regularization term. This regularizer is intended to promote solutions conforming to some notion of simplicity or low complexity. We investigate both noiseless recovery and stability to noise and provide a very general and unified analysis framework that goes far beyond the sparse phase retrieval mostly considered in the literature. In the noiseless case we provide sufficient conditions under which exact recovery, up to global sign change, is possible. For Gaussian measurement maps, we also provide a sample complexity bound for exact recovery. This bound depends on the Gaussian width of the descent cone at the soughtafter vector which is a geometric measure of the complexity of the latter. In the noisy case, we consider both the constrained (Mozorov) and penalized (Tikhonov) formulations. We provide sufficient conditions for stable recovery and prove linear convergence for sufficiently small noise. For Gaussian measurements, we again give a sample complexity bound for linear convergence to hold with high probability. This bound scales linearly in the intrinsic dimension of the sought-after vector but only logarithmically in the ambient dimension.