Low Complexity Iterative 2D DOA Estimation in MIMO Systems
Paper and Code
Mar 15, 2023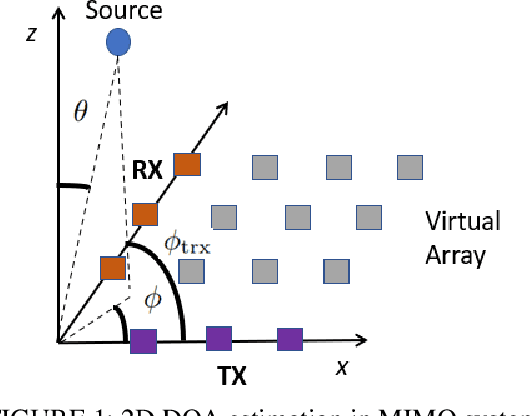
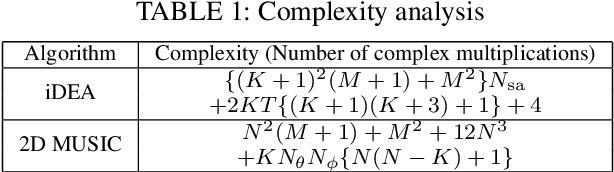
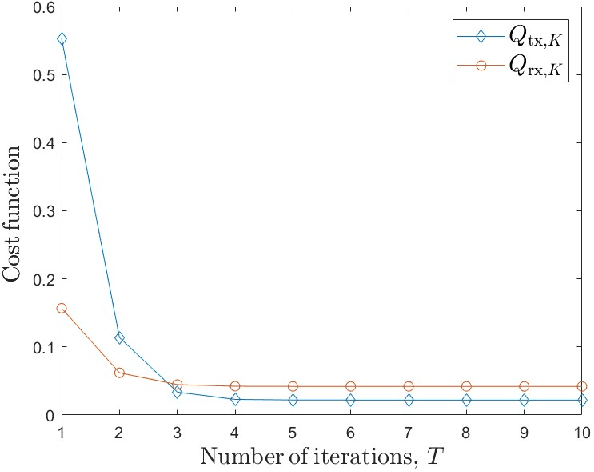
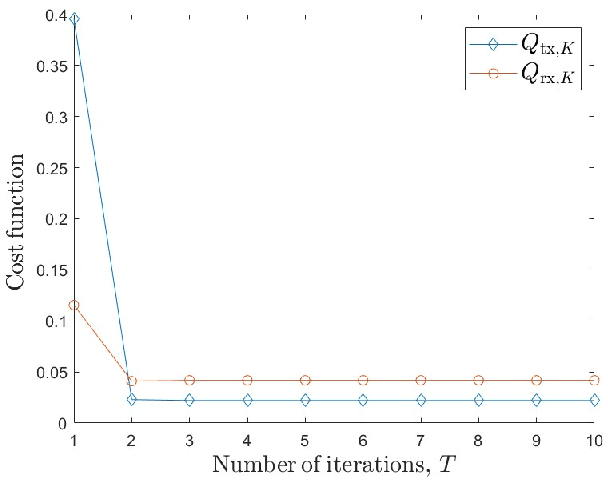
Multiple-input multiple-output (MIMO) systems play an essential role in direction-of-arrival (DOA) estimation. A large number of antennas used in a MIMO system imposes a huge complexity burden on the popular DOA estimation algorithms, such as MUSIC and ESPRIT due to the implementation of eigenvalue decomposition. This renders those algorithms impractical in applications requiring quick DOA estimation. Consequently, we theoretically derive several useful noise subspace vectors when the number of signal sources is less than the number of elements in both the transmitter and receiver sides. Those noise subspace vectors are then utilized to formulate a 2D-constrained minimization problem, solved iteratively to obtain the DOAs of all the sources in a scene. The convergence of the proposed iterative algorithm has been mathematically as well as numerically demonstrated. Depending on the number of iterations, our algorithm can provide significant complexity gain over the existing high-resolution 2D DOA estimation algorithms in MIMO systems, such as MUSIC, while exhibiting comparable performance for a moderate to high signal-to-noise ratio (SNR).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge