Low-Complexity Cramér-Rao Lower Bound and Sum Rate Optimization in ISAC Systems

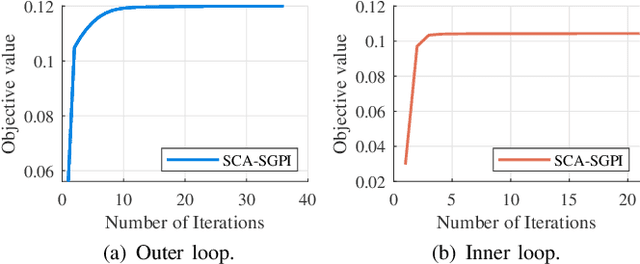
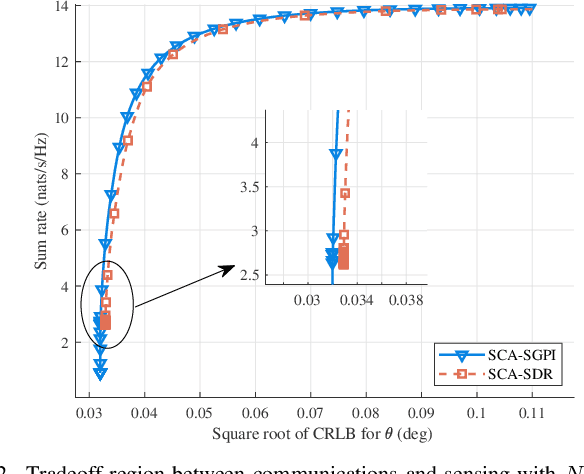
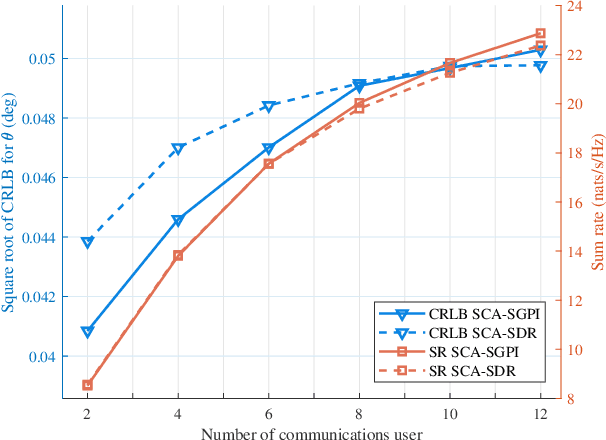
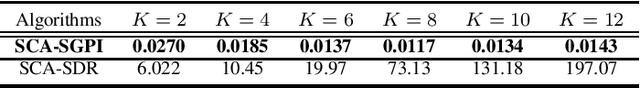
While Cram\'er-Rao lower bound is an important metric in sensing functions in integrated sensing and communications (ISAC) designs, its optimization usually involves a computationally expensive solution such as semidefinite relaxation. In this paper, we aim to develop a low-complexity yet efficient algorithm for CRLB optimization. We focus on a beamforming design that maximizes the weighted sum between the communications sum rate and the sensing CRLB, subject to a transmit power constraint. Given the non-convexity of this problem, we propose a novel method that combines successive convex approximation (SCA) with a shifted generalized power iteration (SGPI) approach, termed SCA-SGPI. The SCA technique is utilized to approximate the non-convex objective function with convex surrogates, while the SGPI efficiently solves the resulting quadratic subproblems. Simulation results demonstrate that the proposed SCA-SGPI algorithm not only achieves superior tradeoff performance compared to existing method but also significantly reduces computational time, making it a promising solution for practical ISAC applications.